Метод координат на плоскости и в пространстве.

Аффинная система координат:

Аффинная система координат (косоугольная система координат) — прямолинейная система координат ваффинном пространстве.

В -мерном пространстве она задаётся упорядоченной системой линейно независимых векторов , выходящих из одной точки .

Аффинными координатами точки называют такие числа 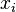, что

Tочку и систему векторов называют репером или аффинным базисом; прямые, проходящие через вектора — координатными осями.

На аффинной плоскости координату называют абсциссой, а — ординатой точки . В пространстве же координаты точки называют её абсциссой, ординатой и аппликатой. Аналогичным образом именуют и координатные оси.

Вычисление координат делящей точки: Если x₁ и y₁ - координаты точки A, а x₂ и y₂ - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении , определяются по формулам

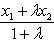
Если 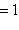, то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам

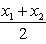
Прямоугольная система координат:

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве.

Преимущества прямоугольной системы координат: Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению.

Нахождение координат вектора через координаты его концов:

Чтобы найти координаты вектора 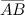, если заданы координаты его начала и конца, необходимо от координат конца отнять соответствующие координаты начала. В случае если точки заданы на плоскости и имеют соответственно координаты и 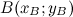, то координаты вектора 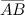вычисляются по формуле:

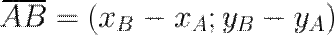
Если точки заданы в пространстве и имеют координаты и соответственно, то координаты вектора 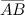вычисляются по следующей формуле:

Нахождение координат точки, делящей отрезок в данном отношении:

Если x₁ и y₁ - координаты точки A, а x₂ и y₂ - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении , определяются по формулам

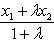
Если 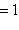, то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам

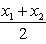
Нахождение длины вектора и отрезка через координаты его начала и конца:

Если на плоскости заданы точки и , то вектор 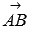имеет координаты и его длина вычисляется по формуле 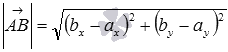, а формула для нахождения длины вектора 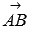по координатам точек и 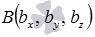трехмерного пространства имеет вид .

Вычисление площади треугольника, заданного координатами его вершин:

Пусть точки A₁(x₁; y₁), A₂(x₂; y₂), A₃(x₃; y₃) - вершины треугольника, тогда его площадь выражается формулой:
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.

Примечание: если определитель равен 0, то это означает, что точки лежат на одной прямой. Таким образом, равенство нулю определителя задает условие, при котором три точки лежат на одной прямой.

Полярные координаты:

Полярная система координат —двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Переход к прямоугольной системе координат:

Прямоугольная система координат на плоскости вводится следующим образом. Возьмем на плоскости две взаимно перпендикулярные числовые оси 0х и 0у, имеющие общее начало точку 0 и общую единицу масштаба.
Оси 0х и 0у образуют прямоугольную (декартовую) систему координат на плоскости.
Проекции точки на плоскости на оси координат, а точнее, их числовые значения, называются прямоугольными или декартовыми прямоугольными координатами точки на плоскости.

Кроме прямоугольных декартовых координат на плоскости существуют другие системы координат, позволяющие определить положение каждой точки плоскости с помощью двух действительных чисел. Наиболее употребительной после декартовой системы координат является полярная система координат.

Возьмем на плоскости точку 0, которую назовем полюсом. Проведем из полюса луч 0р, называемый полярной осью.
Полюс и полярная ось образуют полярную систему координат на плоскости.

Расстояние r от точки до полюса называют полярным радиусом точки . Угол между полярной осью и радиусом называют полярным углом точки.
Полярный радиус и полярный угол называют полярными координатами точки на плоскости.

Уравнение линии:

Уравнением линии называется уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линии и только они.

Входящие в уравнение линии переменные x и y называются текущими координатами, а буквенные постоянные - параметрами.

Чтобы составить уравнение линии как геометрического места точек, обладающих одинаковым свойством, нужно:

1) взять произвольную (текущую) точку M(x, y) линии;
2) записать равенством общее свойство всех точек M линии;
3) входящие в это равенство отрезки (и углы) выразить через текущие координаты точки M(x, y) и через данные в задаче.

Параметрические уравнения линии:

Обозначим буквами х и у координаты некоторой точки М; рассмотрим две функции аргумента t:

, (1)

При изменении t величины х и у будут, вообще говоря, меняться, следовательно, точка М будет перемещаться. Равенства (1) называются параметрическими уравнениями линии, которая является траекторией точки М; аргумент t носит название параметра. Если из равенств (1) можно исключить параметр t, то получим уравнение траектории точки М в виде

F(x, y)=0.

 

4. Скалярное, векторное и смешанное произведения векторов. Приложение к решению задач.

Скаля́рноепроизведе́ние(иногда внутреннее произведение) — операция над двумя векторами, результатом которой является число [когда рассматриваются векторы, числа часто называют скалярами], не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Скалярным квадратом вектора называется его скалярное произведение само на себя и может быть вычислено через модуль вектора:

 

 

Свойства скалярного произведения векторов:

1. Скалярное произведение обладает переместительным свойством: ab=ba

Скалярное произведение векторов в координатной форме:

Теорема. (Скалярное произведение векторов в координатной форме.) Скалярное произведение векторов равно сумме произведений соответствующих координат.

Другими словами, пусть , . Тогда

. (1)

Доказательство. Учитывая, что скалярное произведение ортогональных векторов равно нулю, а скалярный квадрат единичноговектора равен 1 , получаем:

, ч.т.д.

Теорема доказана.

Угол между векторами:

Пусть заданы два произвольных ненулевых вектора и . Приведем их к общему началу, для этого отложим от некоторой точки векторы и , равные соответственно заданным векторам и (рис. 1).

Углом между векторами и называется угол

Угол между двумя векторами , заданными своими координатами, вычисляется по формуле:

Условие перпендикулярности векторов:

· Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.

· Даны два вектора a (xa;ya) и b (xb;yb). Эти векторы будут перпендикулярны, если выражение x_ax_b + y_ay_b= 0.

Приложение скалярного произведения векторов к решению задач:

1. Определение косинуса угла между векторами:

 

.

 

2. Нахождение проекции вектора на заданное направление:

 

, .

 

Определение векторного произведения неколлинеарных векторов:

Вектор называется векторным произведением неколлинеарных векторов и , если:

 

1) его длина равна произведению длин векторов и на синус угла между ними:

2) вектор ортогонален векторам и ;
3) векторы , , (в указанном порядке) образуют правую тройку.

Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

 

Векторное произведение обозначается (или ).

 

Свойства векторного произведения векторов:

Для произвольных векторов и произвольного числа справедливы следующие свойства:

1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.

2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью. Иными словами, порядок векторов имеет значение.

3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?

4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.

Векторное произведение векторов в координатной форме:

Пусть два вектора и разложены по координатным ортам:

Перемножив почленно эти разложения, мы получим:

Отсюда, согласно правилам векторного перемножения ортов, будет следовать

или, после группировки коэффициентов у соответствующих ортов:

.

Полученные коэффициенты при являются определителями второго порядка:

.

Мы видим, что в правой части получился развернутый определитель третьего порядка, элементами первой строки которого являются векторы .

Таким образом:

(2.9)

Это и есть окончательная формула, выражающая векторное произведение в координатной форме.

Площадь треугольника:

1. Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

S =		a · h

2. Формула площади треугольника по трем сторонам