Нахождение определителя n-го порядка.
1. Метод понижения порядка. Нахождение определителя n-го порядка сводится к вычислению п определителей (n – 1)-го порядка. Метод неэффективен.
2. Нахождение определителя сводится к вычислению одного определителя (n – 1)-го порядка. Для этого достаточно все элементы, кроме одного, в каком-либо столбце (строке) сделать равными нулю.
3. Приведение определителя к треугольному виду. Состоит в таком его преобразовании, когда все элементы, лежащие по одну сторону главной диагонали, становятся нулями. Полученный определитель равен произведению элементов главной диагонали
7. Полиномы над полем. Теория делимости.
Полином - это старое название многочлена. Поэтому все, что присуще многочлену, присуще и полиному.
Многочленом от одной переменнойназывается функция, которая может быть представлена в виде:  (сумма степенных функция), где a-свободный член, а0, a1, a2...-некоторые действительные числа.
(сумма степенных функция), где a-свободный член, а0, a1, a2...-некоторые действительные числа.
Сумма, разность и произведение двух многочленов так же являются многочленами.
 Произведение:
Произведение: 
Так как, сумма разность и произведение многочленов является многочленом, то многочлены образуют подкольцо кольца всех функций действительной переменнойи обозначается: R[x].
Определение:два многочлена f(x) и g(x) являются равными, если коэффициенты при соответствующих степенях х равны. Пример: f(x)=g(x);  и
и 
Свойства операций сложения и умножения многочленов:
- Коммутативность сложения: f(x)+g(x)=g(x)+f(x)
- Ассоциативность сложения: f(x)+[g(x)+p(x)]=[f(x)+g(x)]+p(x)
- Дистибутивность умножения относительно сложения: левое: f(x)*[g(x)+p(x)]=f(x)*g(x)+f(x)*p(x); правое: [f(x)+g(x)]*p(x)=f(x)*p(x)+g(x)*p(x).
- Существование нуля. Нулевым многочленомназывается многочлен у которого все коэффициенты равны нулю:

- Существование противоположного элемента: f(x)+[-f(x)]=0(нулевой многочлен).
Выполнение свойств 1-5 означает, что многочлены с действительными коэффициентами сами образуют кольцо относительно операции сложения и умножения.
Определение: Степенью не нулевого многочлена называется наибольшее из числа k таких, что: 
Пример:  (Наибольшая степень х не равная нулю)
(Наибольшая степень х не равная нулю)
 где 5-наибольшая степень х и значит сам многочлен пятой степени.
где 5-наибольшая степень х и значит сам многочлен пятой степени.
 старший член.
старший член.
Многочлен, старший член которого имеет коэффициент равный единице называется нормированным.
Пример:  где при
где при  стоит единица называется нормированным.
стоит единица называется нормированным.
Деление с остатком!
В общем случае в кольце многочленов деление в общем смысле слова как правило не возможно.
Например:  деление на x+1
деление на x+1

Однако, имеется возможность деления с остатком.
Теорема:Пусть f(x)-многочлен с коэффициентами из кольца K. Для любого  многочлен f(x) можно единственным образом представить в виде:
многочлен f(x) можно единственным образом представить в виде:  где С-остаток многочлена, а g(x)-неполное частное.
где С-остаток многочлена, а g(x)-неполное частное.
Определение: Число  называется корнем многочлена f(x) если:
называется корнем многочлена f(x) если: 
Пример: 
Следствие теоремы-теорема Безу: Многочлен f(x) делится на  тогда и только тогда, когда
тогда и только тогда, когда  его корень.
его корень.
Разделить многочлен на двучлен  можно с помощью схемы Горнера.
можно с помощью схемы Горнера.
Пример: Разделить многочлен  на двучлен
на двучлен 
1;(  ;не изменяется ;не изменяется
| 0;  ;(2*1)+0 ;(2*1)+0
| -3;  ;(2*2)-3 ;(2*2)-3
| 1;(x); (2*1)+1 | 5;  ;(2*3)+5 ;(2*3)+5
| |
| 2;(x=2) |
 , C=1
, C=1

Для двух многочленов f(x) и g(x) можно найти многочлены p(x) и r(x) такие, что будет справедливо равенство:

Причем степень r(x) меньше степени g(x). r(x)-остаток от деления.
Определение:НОД(наибольший общий делитель) отличный от нуля многочленов f(x) и g(x) является многочлен d(x) который является их общим делителем и вместе с тем сам делится на любой другой общий делитель этих многочленов.
Для нахождения НОД используется алгоритм Евклида: Пусть даны многочлены f(x) и g(x). Делим f(x) на g(x) и получаем остаток  . Затем делим g(x) на
. Затем делим g(x) на  получаем остаток
получаем остаток  .
.  делим на
делим на  и т.д. пока не получим НОД, т.е. остаток будет равен нулю.
и т.д. пока не получим НОД, т.е. остаток будет равен нулю.
8. Разложение полинома в произведение неприводимых множителей и его единственность.
Определение:Ненулевой элемент называется простым, если он не может быть разложен в произведение двух не обратимых элементов.
Простые элементы кольца многочленов называютсянеприводимыми многочленами, поскольку не обратимые элементы кольца многочленов отличны от нуля это многочлены положительной степени,то неприводимый многочлен, это такой многочлен положительной степени, который не может быть разложен в произведение двух многочленов положительной степени.
Определение: Многочлен, который может быть разложен в произведение двух многочленов положительной степени называется приводимым.
Определение: Неприводимый многочлен, такой многочлен положительной степени, который не может быть разложен в произведение двух многочленов меньшей степени.
Пример:  -приводимый, а
-приводимый, а  неприводимый.
неприводимый.
Теорема:Всякий многочлен, не являющийся элементом поля может быть разложен в произведение неприводимых многочленов.
Пример:  , где P(x) приводится следующим образом
, где P(x) приводится следующим образом  .
.
Если вынести за скобку старшие коэффициенты всех не приводимых множителей какого-либо разложения многочлена, то многочлен представится в виде: 
Такое представление называется нормированным разложениемна неприводимые множители.
Пример:  многочлен не приводим над полем действительных чисел, тк как D(дискриминант)=-3, тогда решение будет находится в поле комплексных чисел:
многочлен не приводим над полем действительных чисел, тк как D(дискриминант)=-3, тогда решение будет находится в поле комплексных чисел:

Множитель  присутствует в нормированном разложении многочлена P(x) на неприводимые множители тогда и только тогда, когда
присутствует в нормированном разложении многочлена P(x) на неприводимые множители тогда и только тогда, когда  корень многочлена P(x), при этом кратность множителя
корень многочлена P(x), при этом кратность множителя  равно кратности корня
равно кратности корня  .
.
Таким образом, число множителей первой степени в разложении многочлена P(x) на неприводимые множители равно числу его корней(с учетом кратности).
Многочлен степени 2 или 3 неприводим тогда и только тогда, когда он не имеет корней в данном поле.
9. Векторные пространства. Примеры и простейшие свойства векторных пространств. Подпространство.
Пусть p-некоторое поле.
Элементами данного поля могут быть как числа, так и другие объекты.
Определение: Множество V-называется векторным(линейным) пространствомнад полем p, если:
1) на V определена операция, называемая сложением:каждым двум элементам a,b 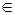 V становится в соответствие элемент a+b из этого же пространства.
V становится в соответствие элемент a+b из этого же пространства.
2) Определена операция называемая умножениемэлементов из V на числа из поля p, при a 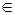 V,
V,  , где
, где  число,
число,  p (множество действительных чисел), в котором
p (множество действительных чисел), в котором  становится в соответствие элемент
становится в соответствие элемент  .
.
3) Эти операции удовлетворяю следующим свойствам: a,b,c 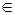 V,
V,  :
:
а) a+b=b+a-свойство коммутативности
б) a+(b+c)=(a+b)+c-свойство ассоциативности
в)  (квантор существования, EXISTENS):
(квантор существования, EXISTENS):  -существует нулевой элемент такой что: a+0=a
-существует нулевой элемент такой что: a+0=a
г)  (Для любого элемента a существует единственный (!) противоположный элемент (-a) такой что (-a)+a=0.
(Для любого элемента a существует единственный (!) противоположный элемент (-a) такой что (-a)+a=0.
д) 
е) 
ж) 
з) 
Если выполняются все эти свойства то пространство векторное.
Простым случаем векторного пространства является арифметическое пространство. Например:трехмерное пространство состоящее из векторов  .
.
Пример: множество матриц двумерного пространства:




 ,
, 