Сопряжение двух прямых
Центр дуги сопряжения должен быть равноудален (находится на одинаковом расстоянии) от каждой из двух сопрягаемых (данных) прямых. Любая из точек сопряжения (точки входа) представляет собой пересечение перпендикуляра, опущенного из центра сопряжения на соответствующую прямую.
Алгоритм построения сопряжения двух прямых дугой заданного радиуса (рис. 13.39, а, б) следующий:
1. На расстоянии (R), равном радиусу дуги сопряжения, проводятся две прямые, параллельные сопрягаемым прямым.
2. Определяют их точку пересечения, являющуюся центром сопряжения (О).
3. Из точки (О) проводят перпендикуляры к заданным прямым и находят точки сопряжения (А) и (В).
4. Из точки (А) к точке (В) строят дугу сопряжения заданного радиуса (R).

Рисунок 13.49
Типичными примерами сопряжений являются контуры деталей, изображенных на рис. 13.40.
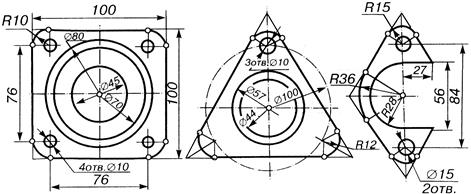
Рис. 13.40.
В AutoCAD сопряжение двух отрезков прямых (рис. ХХ а) выполняется командой «Сопрячь» (Скругление, Шпонка, Fillet) из меню «Модификация». После выбора команды следует параметром «Radius» задать радиус сопряжения (например, 10 мм), затем последовательно указателем мышки отметить оба отрезка (см. рис. ХХ б).
Command:
FILLET
Current settings: Mode = TRIM, Radius = 5.0000
Select first object or [Polyline/Radius/Trim]: radius
Specify fillet radius <5.0000>: 10
Select first object or [Polyline/Radius/Trim]:
Select second object:
Полученный элемент состоит из двух исходных отрезков и дуги сопряжения R=10мм (см. рис. ХХ в).

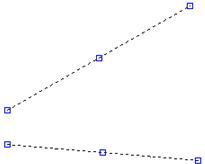

Рис. ХХ а) Рис. ХХ б) Рис. ХХ в)
1.2. Сопряжение дуги окружности радиуса R и прямой а с дугой заданного радиуса R1
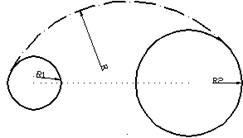
Для выполнения этого сопряжения (рис. 3.31) сначала определяют множество центров дуг радиуса R1. Для этого на расстоянии R1 от прямой а проводят параллельную ей прямую m, а из центра О радиусом (R + R1) – дуги концентрической окружности. Точка О1 будет центром дуги сопряжения. Точка сопряжения С получена на перпендикуляре, опущенном из точки О1 на прямую а, а точка В – на прямой, соединяющей точки О и О1.
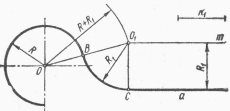
Рисунок 3.31
На рис. 3.32 представлен пример изображения контура подшипника, в построении которого использован рассмотренный вид сопряжений.

Рисунок 3.32
Сопряжение прямой и окружности в AutoCAD имеет смысл при построении к окружности отрезка прямой, являющейся касательной к этой окружности. Для этого при построении отрезка начальную точку отрезка задают по координатам или объектной привязкой, конечную точку задают привязкой «Касательная» (Прыжок в тангенс) относительно окружности (работа с привязкой описана в приложении ХХХХХХХХХХХ).
1.3. Сопряжение дуг двух окружностей с радиусами R1 и R2, дугой сопряжения радиуса R
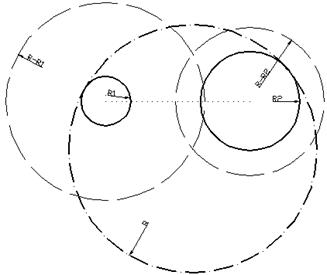
Различают внешнее (рис. 13.42,а), внутреннее (рис. 13.42, б) и смешанное (рис. 13.42, в) сопряжения. В первом случае центр сопряжения является точкой пересечения дуги окружностей радиусов R1+R и R2+R, во втором - на пересечении окружностей радиусов R-R1 и R-R2, в третьем - на пересечении дуг окружностей радиусов R+R1 и R-R2. Точки сопряжения А1 и А2 лежат на прямых, соединяющих центр сопряжения с центром соответствующей окружности.

Рассмотрим случай внешнего сопряжения двух окружностей в AutoCAD. На рис. ХХ.а показаны две опорные окружности с радиусами R1 и R2, центры которых лежат на концах пунктирной линии. Из центра окружности R1 строят вспомогательную окружность с радиусом R1+R, а из центра окружности R2 – окружность R2+R как это показано на рис. ХХ.б (вспомогательные окружности показаны штриховой линией). Затем из точки пересечения вспомогательных окружностей строят окружность с радиусом R (на рис. ХХ в показана штрих-пунктирной линией). Окончательные построения выполняют с помощью команды «Обрезать» из меню «Модификация». В качестве секущих объектов выбирают опорные окружности и обрезают верхнюю часть окружности R, затем удаляют вспомогательные окружности (результат построения показан на рис. ХХ.г).
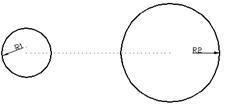

Рисунок ХХ.а Рисунок ХХ.б


Рисунок ХХ.в Рисунок ХХ.г
Теперь рассмотрим случай внутреннего сопряжения двух окружностей в AutoCAD. Аналогично предыдущему случаю строят опорные окружности с радиусами R1 и R2. Из центра окружности R1 строят вспомогательную окружность с радиусом R–R1, а из центра окружности R2 – окружность R–R2. Затем из точки пересечения вспомогательных окружностей строят окружность с радиусом R (см. рис. ХХХ.а). Лишние элементы удаляют аналогично предыдущему случаю (результат показан на рис. ХХХ.б).