Решение обратной задачи

Решение обратной задачи заключается в нахождении параметров объекта по распределению магнитного поля. Искомые параметры – глубина залегания центра шара и его радиус. При решении используется метод характерных точек. Исходя из приведенных формул можно заключить, что кривая Z_a имеет максимум в точке х=0. Если Z_a=0, то в ноль должен обращаться числитель 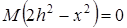, при этом момент обращаться в ноль не может, а значит получаем:

.

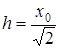Из формулы для Z_a находим радиус объекта:

, отсюда 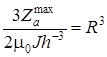, тогда

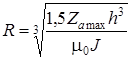
Радиус находят в том случае, если известна намагниченность J. В данной работе берется значение намагниченности, которое использовалось при решении прямой задачи.

Найти в учебнике А.А. Логачёва 4 способа определения определения глубины центра шара по графикам Z_a и Н_а

Составить структурированный отчёт по лабораторной работе.

 

Варианты

Вар.	h, м	R, м	J, А/м
			0,5
			0,5
			0,5
			0,5
			0,6
			0,6
			0,6
			0,6
			0,7
			0,7
			0,7
			0,7

 

			0,8
			0,8
			0,8
			0,8
			0,9
			0,9
			0,9
			0,9