Исследование зависимости показателей качества, измеряемых в нечисловых шкалах
Пусть проводится оценка объекта по двум качественным характеристикам X и Y. Для каждой из них используется соответствующее конечное множество пунктов нечисловых шкал
SX = { s1, s2, … , sp} ,
и
SУ = { t1, t2, … , tq}.
Следовательно, элементы множеств SX и SУ рассматриваются как возможные значения двух нечисловых переменных: соответственно X и Y, которые являются показателями, характеризующими качество изучаемых объектов.
Пусть значения данных показателей оценивались для каждого из объектов некоторой совокупности, общее число элементов которой обозначим через n. Введем, кроме того, следующие обозначения:
ni,* – общее число объектов, результат оценки которых по показателю X, равен si (i = 1,…, p);
n*,j – общее число объектов, результат оценки которых по показателю Y, равен tj (j = 1,…, q);
ni,j – число объектов, у которых значение (уровень качества) показателя X равно si , а значение показателя Y равно tj .
Числа ni,j называют совместными частотами, с которыми наблюдается данное сочетание возможных значений показателей X и Y, а ni,* и n*,j – маргинальными частотами значений показателей X и Y соответственно.
Как легко убедиться, будут справедливы следующие соотношения:
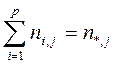 ; (28)
; (28)
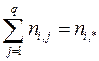 ; (29)
; (29)


 . (30)
. (30)
Матрицу N = {ni,j }, составленную из элементов ni,j , имеющую размеры p×q, будем называть таблицей сопряженности результатов измерения показателей X и Y на данном множестве объектов.
Отношения, определяемые равенствами
pi,j = ni,j / n , (31)
pi,* = ni,* / n , p*,j = n*,j / n , (32)
представляют собой:
- совместные относительные частоты, с которыми у объектов из данной совокупности наблюдались, значения показателей X = si и Y = tj ;
- маргинальные относительные частоты значений (X = si ), (Y = tj ) показателей Xи Y соответственно;
Относительные частоты (31) и маргинальные относительные частоты (32) можно (в силу закона больших чисел) рассматривать как приближенные оценки вероятностей того, что объект, взятый наудачу из данной совокупности, будет иметь указанные значения показателей Xи Y.
Таблица сопряженности в отдельных случаях сама по себе позволяет сделать определенные выводы о наличии (или об отсутствии) связи между данными двумя показателями качества рассматриваемых объектов.
Пример. Одно из вкусовых качеств 20 виноградных вин, произведенных из винограда, собранного в трех различных регионах: s1, s2, s3 , оценивалось по 4-балльной ординальной шкале, имеющей пункты: t1 – «высокое», t2 – «выше среднего», t3 – «среднее», t4 – «недостаточное». Пусть таблица сопряженности имеет вид, представленный в таблице 5.
Табл.5.
 Х У Х У
| t1 | t2 | t3 | t4 |
| s1 | ||||
| s2 | ||||
| s3 |
Даже не прибегая к сложным вычислениям, с помощью таблицы 5 легко проследить существующую зависимость рассматриваемого вкусового показателя Y от региона сбора винограда X. Так, все образцы вин, выращенные в регионе s1, обладают высоким уровнем данного вкусового качества (t1). Все без исключения образцы, у которых этот уровень «средний», выращены в регионе s3. Кроме того, среди образцов, имеющих уровень «выше среднего», подавляющее большинство (80%) выращены в регионе s2 . Наконец, из таблицы 5 можно сделать и тот вывод, что данный вкусовой показатель в среднем выражен слабее у вин из региона s3, чем у вин из региона s2.
Представляет интерес получение ответа на вопрос: независимы ли показатели Xи Y. Для проверки гипотезы о независимости показателей Xи Y могут использоваться как таблица сопряженности N= {ni,j}, так и матрица совместных относительных частот P = { pi,j }, элементы которой легко могут быть найдены согласно (31). Рассматривая матрицу P в качестве оценки совместного распределения данных двух нечисловых показателей Xи Y, можно воспользоваться известным из теории вероятностей условием независимости дискретных случайных величин, а именно Xи Y являются независимыми, если для всех i = 1,…, p и всех j = 1,…, q выполняется равенство
pi,j = pi,* p*,j (33)
При этом, как известно, отношение pi,j/pi,* служит оценкой вероятности того, что показатель Y примет свое возможное значение tj при условии, что показатель X принял значение si . Значения
pi,1/ pi,* , pi,2/ pi,* , …, pi,q / pi,* (34)
представляют собой условное распределение Y при условии, что X = si . При выполнении условия (33) условное распределение (2.34) в точности совпадает с безусловным, т. е. маргинальным распределением Y
p*,1 , p*,2 , …, p*,q (35)
Таким образом, проверяемая гипотеза состоит в том, что распределение частот, с которыми в данной совокупности встречаются возможные значения одного из показателей, не зависит от того значения, который принял другой.
Разумеется, точное выполнение условия (33) для всех i и j на практике встречается крайне редко. Поэтому разности
pi,j - pi,* p*,j =  =
=  (ni,j - ni,* n*,j / n )
(ni,j - ni,* n*,j / n )
могут рассматриваться как меры отклонения реальных данных от проверяемой гипотезы (33). Установлено, что если X и Y независимы, то величина
χ2расчет =  (36)
(36)
подчиняется распределению “хи-квадрат” с (p-1)×(q-1) степенями свободы.
Если при заданном уровне значимости α (на практике его часто выбирают равным 0.05 [115]) значение χ2расчет превосходит α-процентную точку χ2табл распределения χ2 с (p-1)(q-1) степенями свободы, т.е.
χ2расчет > χ2табл ,
то гипотезу о независимости показателей X и Y следует отвергнуть. В противном случае будем говорить, что имеющиеся данные результатов измерения показателей не противоречат проверяемой гипотезе и, следовательно, отвергать ее нет оснований.
Напомним, что если рассматриваемый показатель измеряется в шкале наименований, то в результате измерения на данном множестве объектов устанавливается отношение эквивалентности, а если он измеряется по ординальной шкале, то устанавливаемое отношение является квазипорядком.
Мера «похожести» двух бинарных отношений R(X) и R(Y), определяемых показателями X и Y, вычисляется по формуле
d(R(X) , R(Y)) = 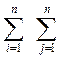 ç r(X)i,j - r(Y)i,j ç, (37)
ç r(X)i,j - r(Y)i,j ç, (37)
где R(X) = { r(X)i,j}, R(Y) = { r(Y)i,j} – матрицы бинарных отношений R(X) и R(Y), обе имеющие размеры n·n, где n – число объектов в данной совокупности.
С добавлением новых объектов размеры обеих матриц возрастают, что на практике при большом числе объектов приводит к существенным неудобствам. С этой точки зрения таблица сопряженности N= { ni,j }, с размерами p×q, имеет ряд преимуществ: ее размеры, как правило, невелики, так как различных возможных уровней показателей качества Xи Y на практике не бывает много. Кроме того, добавление новых объектов не изменит значения p и q (за исключением тех случаев, когда число пунктов шкалы измерения показателя заранее неизвестно).
Рассмотрим вопрос о том, какой вид приобретает формула (37) для вычисления расстояния между результатами измерения показателей X и Y, в тех частных случаях, когда оба они измеряются по шкале наименований или по ординальной шкале и выразим это расстояние через элементы таблицы сопряженности.
return false">ссылка скрытаПусть N= { ni,j } - таблица сопряженности результатов измерения показателей X и Y, которые оба измеряются по шкале наименований. Тогда можно доказать (см. работу, например, [116], что расстояние (37) между отношениями эквивалентности R(X) и R(Y), порождаемыми результатами измерений, будет иметь следующий вид:
d(R(X), R(Y)) =  (38)
(38)
Если оба показателя X и Y измеряются по ординальной шкале, то расстояние между бинарными отношениями R(X) и R(Y) может быть представлено с помощью элементов таблицы сопряженности в следующем виде:
d(R(X), R(Y)) =  . (39)
. (39)
С помощью таблиц сопряженности и формул (38), (39) можно легко находить расстояния между качественными показателями. В случае, когда имеется несколько таких показателей: X1, X2, …, Xg, попарные расстояния между ними можно представить с помощью матрицы D = {di,j} (i,j = 1,…, g), элементы которой определяются равенством:
di,j = d(R(i), R(j)) , (40)
где R(i) – бинарное отношение, порождаемое показателем Xi (i = 1,…, g).
Такой случай имеет место, например, когда качество оценивалось комитетом из g экспертов, то есть были получены g различных ранжировок одного и того же множества объектов.
Для элементов матрицы D будут выполняться очевидные условия:
di,i = 0 ; di,j = dj,i , (i,j = 1,…, g).
Анализ матрицы D иногда приводит к выводу, что показатели естественным образом разбиты на несколько групп, так что расстояния внутри одной группы относительно невелики, а расстояния между группами существенно больше. Более детальное рассмотрение состава таких групп может позволить найти объяснение этому факту и даже найти интерпретацию каждой из выделенных групп показателей. Таким образом, исследование матрицы D есть один из возможных способов анализа структуры данного множества показателей качества.
Естественным образом возникает задача о построении такого показателя X*, что отвечающее ему бинарное отношение R(*) будет обладать следующим свойством: сумма расстояний от R(*) до бинарных отношений R(i) является минимальной. Это условие можно записать в виде
min 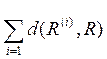 =
=  ,
,
где минимум берется по всевозможным бинарным отношениям R.
Если отношение R(*), обладающее вышеуказанным свойством, удастся построить, то показатель X* можно рассматривать в качестве усредненного показателя, который представляет собой некий компромисс между всеми исходными показателями X1, X2, …, Xg.
Обозначим через {r*j,k} матрицу бинарного отношения R(*) и аналогичным образом через {r (i)j,k} (i = 1,…, g) – матрицы отношений R(i), где j, k = 1,…, n – число оцениваемых объектов. Тогда для искомого отношения R(*) должно выполняться то условие, что сумма
F (R(*) ) = 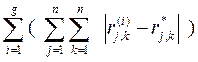 (41)
(41)
принимает минимальное значение по всем {r*j,k}.
Пусть cj,k - число показателей (среди рассматриваемых X1, X2,…, Xg), по которым j-й объект не хуже, чем k-й объект (j, k = 1,…, n). Тогда
cj,k = 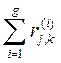 . (42)
. (42)
Поскольку все элементы r*j,k и r (i)j,k могут принимать только значения 0 или 1, то
(r*j,k)2 = r*j,k , (r (i)j,k)2 = r (i) j,k . (43)
Поэтому в (41) можно заменить модуль разности çr (i)j,k - r*j,k ç на квадрат разности (r (i)j,k - r*j,k)2. Тогда (41) можно записать в виде
F(R(*) ) = 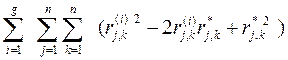 =
=
= 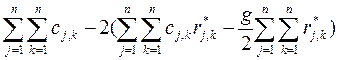 (44)
(44)
Последнее равенство записано с использованием (42) и (43). Выбор отношения R(*) может повлиять только на величину вычитаемого в круглых скобках в выражении (44). Поэтому минимум F(R(*)) достигается тогда, когда достигается максимум выражения
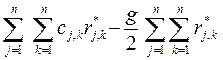 =
= 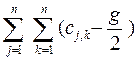 r*j,k . (45)
r*j,k . (45)
Чтобы (45) достигало своего максимума, нужно, чтобы r*j,k равнялось единице всякий раз, когда cj,k > g/2 , и равнялось нулю в противном случае.
Таким образом, мы получили следующее простое правило построения матрицы {r*j,k} искомого бинарного отношения R(*):
 |
1, если cj,k > g/2;
r*j,k = 0, если cj,k < g/2 . (46)
Данное правило можно назвать «правилом большинства», так как оно определяет, что произвольные два объекта из рассматриваемого множества будут находиться в отношении R(*) в том случае, если число исходных отношений R(i) (i = 1,…, g), которые справедливы для данных двух объектов, – более половины от их общего числа g.
К сожалению, на практике данный простой метод построения такого оптимального (усредненного) показателя X* оказывается применимым далеко не всегда. Дело в том, что, как мы помним, исходные показатели X1, …, Xg, как правило, представляют собой признаки объектов, измеряемые по ординальной или номинальной шкале. Соответственно порождаемые ими на данном множестве объектов бинарные отношения R(1), R(2), …, R(g) являются или отношениями эквивалентности, или отношениями квазипорядка. В то же время построенное согласно (2.46) бинарное отношение R(*) вовсе не обязательно будет того же типа, что и отношения R(i) (i = 1,…, g). Для иллюстрации этого обстоятельства можно привести следующий пример.
Пример. Пусть произведена оценка качества пяти объектов по трем показателям X1, X2, X3, которые измеряются по ординальной шкале (например, ранжировка объектов тремя различными экспертами). Предположим, что результаты оценивания имеют следующий вид:
X1 : 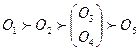 ;
;
X2 : 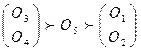 ;
;
X3 :  .
.
Построим матрицы бинарных отношений квазипорядка, которые отвечают показателям X1, X2, X3 :
 |  | ||||||||||
 |  |  | |||||||||
 | |||||||||||
1 1 1 1 1 1 1 0 0 0 1 0 0 1 1
0 1 1 1 1 1 1 0 0 0 1 1 0 1 1
R(1) = 0 0 1 1 1; R(2) = 1 1 1 1 1 ; R(3) = 1 1 1 1 1 .
0 0 1 1 1 1 1 1 1 1 0 0 0 1 1
0 0 0 0 1 1 1 0 0 1 0 0 0 1 1
 Далее согласно критерию (46) построим итоговое бинарное отношение R(*):
Далее согласно критерию (46) построим итоговое бинарное отношение R(*):
1 1 0 1 1
1 1 0 1 1
R(*) = 1 1 1 1 1.(47)
0 0 1 1 1
0 0 0 0 1
Нетрудно показать, что отношение R(*) уже не является квазипорядком. В самом деле, из (47), в частности, следует, что (О4 , О3)ÎR(*) и (О3 , О1)ÎR(*) , но при этом (О4 , О1)ÏR(*). Это в свою очередь означает, что отношение R(*) не обладает свойством транзитивности, а значит, не удовлетворяет определению отношения квазипорядка.
В то же время можно заметить, что если в данном примере объекты О3 и О4 были бы различимы, а именно: О3 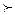 О4 хотя бы по одному из двух показателей X1 или X2, то в (47) r*4,3 будет равно нулю. А этого достаточно для того, чтобы R(*) было бы квазипорядком следующего вида:
О4 хотя бы по одному из двух показателей X1 или X2, то в (47) r*4,3 будет равно нулю. А этого достаточно для того, чтобы R(*) было бы квазипорядком следующего вида:
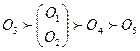 .
.