распределения. Математическое ожидание и дисперсия. Графическое представление. Примеры.
Непрерывные и дискретные случайные величины. Плотность вероятности. Нормальный закон
распределения. Математическое ожидание и дисперсия. Графическое представление. Примеры.
Дискретные величины могут принимать конечное, счетное число случайных событий. (Год рождения студента, число людей в автобусе, число страниц во взятой наугад книге)
Непрерывные величины принимают бесконечное число возможных значений в конечном, или бесконечном интервалах изменения. (время, масса, объем)
Плотностью вероятностиf(x) непрерывной случайной величины Х называется производная функции распределения F(X) этой величины: f(x)=F’(X)
Нормальное распределение (распределение ГАУССА)
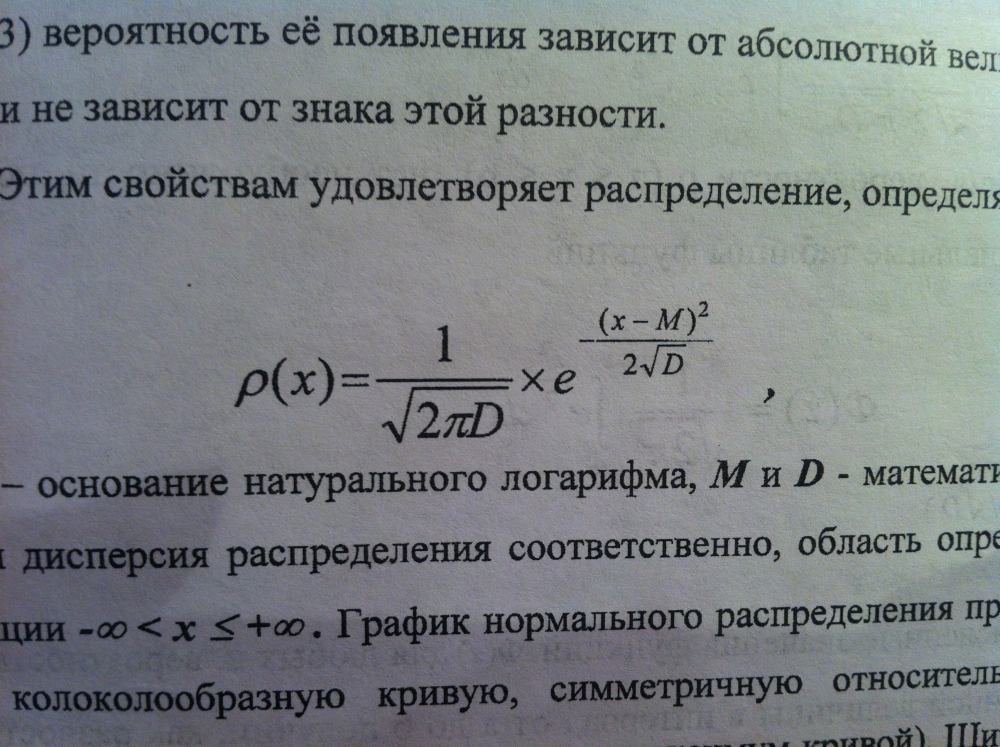
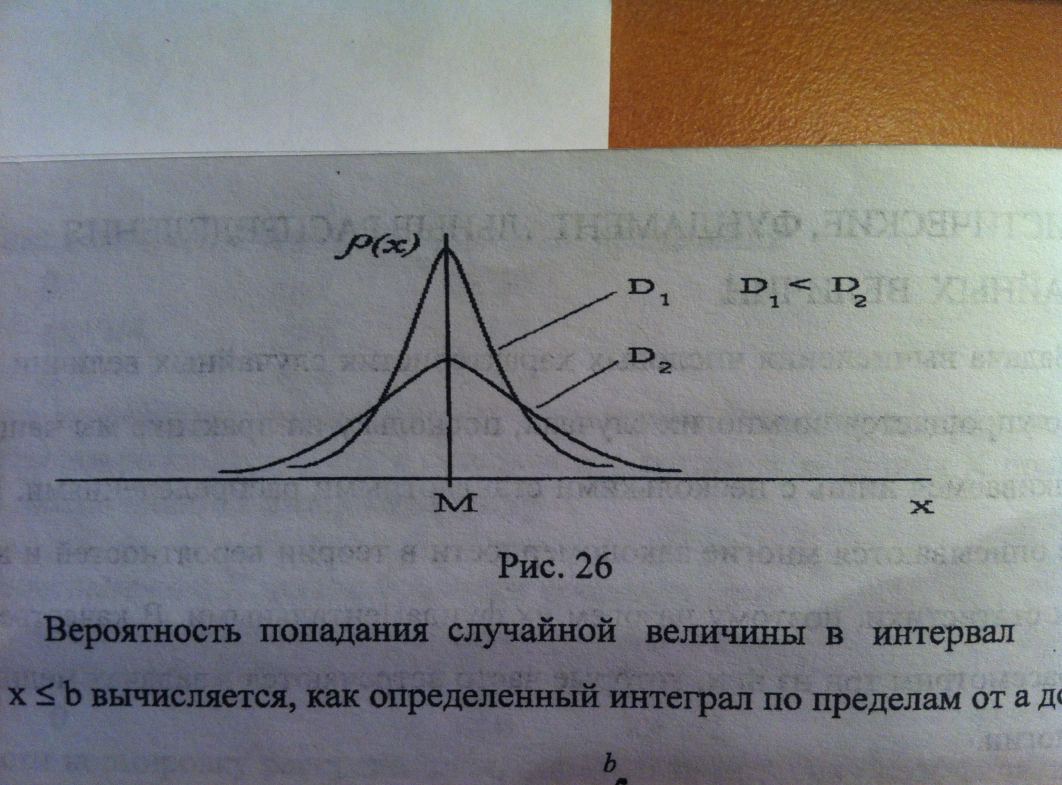
Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случайных величин оно определяется, как сумма произведений случ. величины на вероятность её появления:

Например, в задаче с игральным кубиком вероятности появления цифр с 1 до 6 одинаковы и равны 1/6, поэтому:
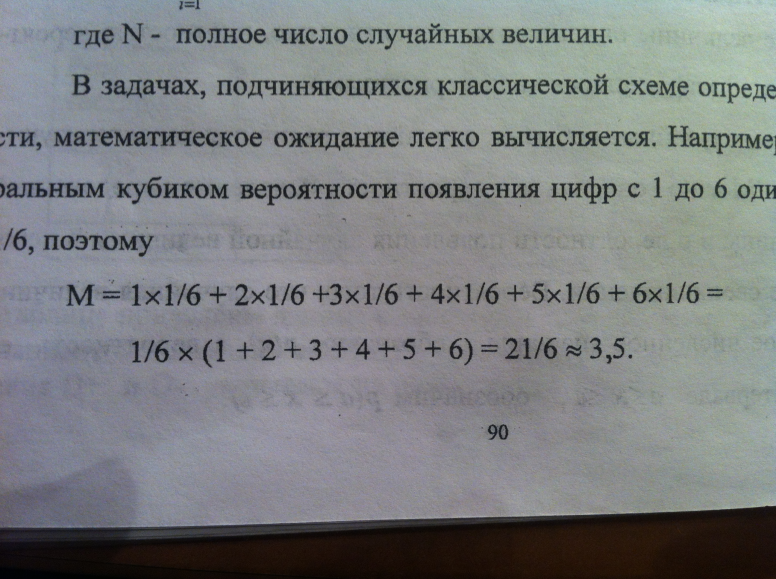
Для непрерывных случайных величин:


Область определения случ. величин может представлять собой и бесконечный интервал
-∞< х<+∞, тогда
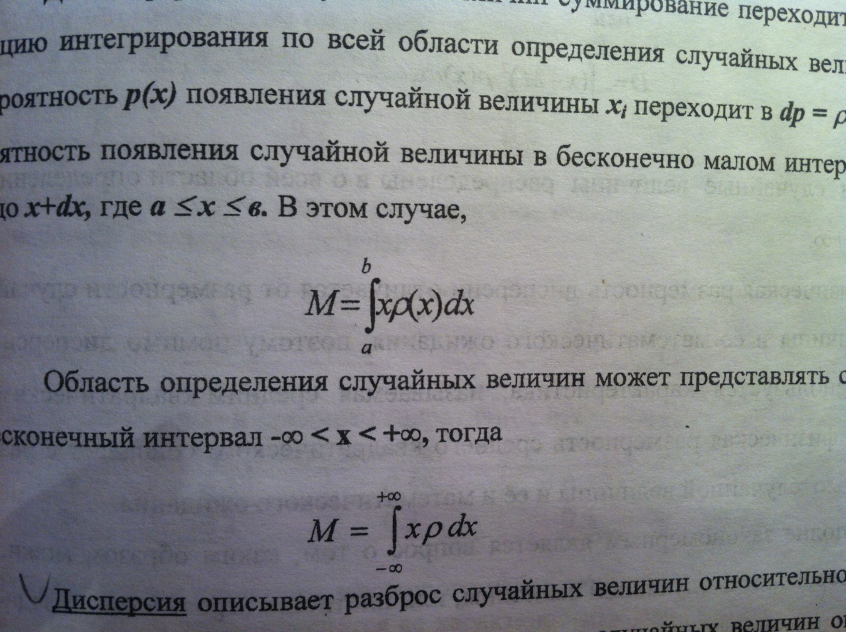
Дисперсия описывает разброс случ. величин относительно математического ожидания. Дисперсия дискретных случ. величин определяется, как сумма квадратов разности случ. величин и математического ожидания на соответствующие вероятности появления этих случайных величин:

В задаче с игральным кубиком: 
В задачах с непрерывными случайными величинами, дисперсия вычисляется по формуле 
Если случ величины распределены во всей области определения -∞< х<+∞, тогда
