ГИСТОГРАММА

Гистограмма, это способ представления статистических данных в графическом виде – в виде столбчатой диаграммы. Она отображает распределение отдельных измерений параметров изделия или процесса. Иногда ее называют частотным распределением, так как гистограмма показывает частоту появления измеренных значений параметров объекта.

Высота каждого столбца указывает на частоту появления значений параметров в выбранном диапазоне, а количество столбцов – на число выбранных диапазонов.

Важное преимущество гистограммы заключается в том, что она позволяет наглядно представить тенденции изменения измеряемых параметров качества объекта и зрительно оценить закон их распределения. Кроме того, гистограмма дает возможность быстро определить центр, разброс и форму распределения случайной величины. Строится гистограмма, как правило, для интервального изменения значений измеряемого параметра.

Порядок построения гистограммы следующий:

1. Собираются статистические данные – результаты измерений параметра объекта. Для того, чтобы гистограмма позволяла оценить вид распределения случайной величины предпочтительно иметь не менее тридцати результатов измерений.

2. Выявляется наибольшее и наименьшее значение показателя среди полученных результатов измерений.

3. Определяется ширина диапазона значений показателя – из наибольшего значения показателя вычитается наименьшее значение.

4. Выбирается надлежащее число интервалов в пределах которых необходимо сгруппировать результаты измерений.

5. Устанавливаются границы интервалов. Границы интервалов необходимо установить так, чтобы значения данных не попадали ни на одну из границ интервала. Например, если были выбраны интервалы с границами от 0,5 до 5,5 от 5,5 до 10,5 и т.д. то значение данных 5,5 будет попадать как в первый, так и во второй интервал. Чтобы избежать этой проблемы можно изменить интервалы от 0,51 до 5,50 от 5,51 до 10,50 и так далее, таким образом ни одно значение данных не попадет на границу интервала.

6. Подсчитывается число попаданий значений результатов измерений в каждый из интервалов.

7. Строится гистограмма – на оси абсцисс (горизонтальной оси) отмечаются интервалы, а на оси ординат (вертикальной оси) отмечается частота попаданий результатов измерений в каждый интервал. Интервалы можно устанавливать в натуральных единицах (если позволяет масштаб), т.е. в тех единицах, в которых проводились измерения, либо каждому интервалу можно присвоить порядковый номер и отмечать на оси абсцисс номера интервалов. В результате получается столбчатая диаграмма, представленная на рисунке ниже.

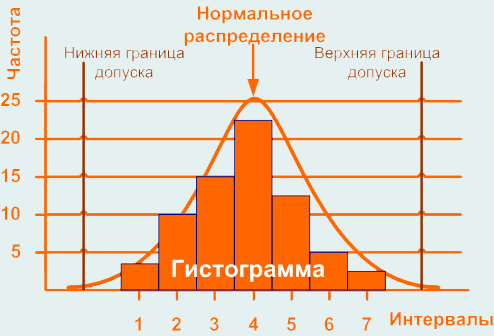
Если на контролируемый параметр существует поле допуска, то гистограмма может содержать верхнюю и нижнюю границы поля допуска. Это позволяет увидеть в какую сторону и как смещается значение контролируемого показателя относительно поля допуска. Границы наносятся по оси абсцисс.

Гистограмма, представленная на рисунке выше имеет форму нормального распределения, что говорит о стабильности процесса, но часто бывает, что форма распределения отклоняется от нормального. Это свидетельствует о нарушениях в процессе и необходимости применения управляющих воздействий. Некоторые, часто встречающие отклонения и их причины представлены ниже.

Гистограмма смещена влево (асимметрия влево):

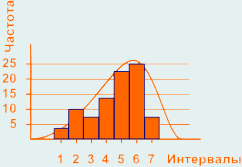Может вызываться смещением процесса к верхней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы верхней границы допуска, либо природа процесса физически запрещает любые измерения больше чем максимальные значения допуска.

 

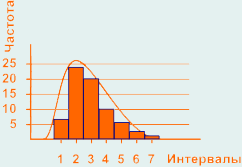Гистограмма смещена вправо (асимметрия вправо):

Может вызываться смещением процесса к нижней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы нижней границы допуска, либо природа процесса физически запрещает любые измерения меньше чем минимальные значения допуска.

 

 

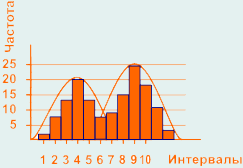Бимодальность:

Гистограмма отображает два совмещенных процесса. Такая ситуация может произойти если результаты измерений получены от двух разных устройств, двух операторов, контролеров, разных измерительных инструментов, или с разных точек измерения.

 

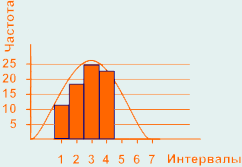Гистограмма усечена:

Распределение не является нормальным т.к. нет постепенного снижения частоты результатов измерений от центра к границам допуска. Такой вид гистограммы возникает если процесс не способен удовлетворять спецификациям и часть измерений отсортирована с двух сторон при приближении к границам допуска, либо потеряны чересчур малые значения результатов измерений.

 

 

Гистограмма не имеет центра:

Центр распределения был отсортирован из набора данных результатов измерений. Такая ситуация может возникнуть из-за недостаточных требований в инженерной спецификации.

 

 

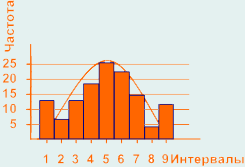Гистограмма содержит выступы на границах:

Часть измерений на удаленных от центра сторонах распределения была изменена, чтобы привести характеристики процесса в соответствие с установленным полем допуска или измерения, выходящие за пределы поля допуска были записаны как входящие в поле допуска.

 

По результатам тестирования по математике учащихся 7-го класса получены данные о доступности заданий теста (отношение числа учащихся, правильно выполнивших задания, к числу тестировавшихся учащихся), предствленные ниже, в таблице.
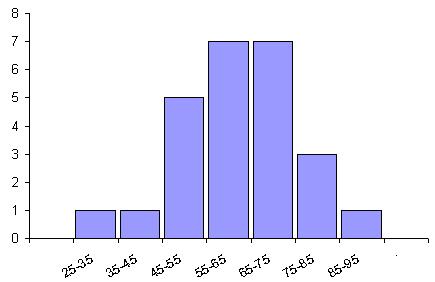
Тест содержал 25 заданий. Построить гистограмму.

Доступность задания x, %	25-35	35-45	45-55	55-65	65-75	75-85	85-95
Количество задач n

 

Решение.

Откладываем на оси абсцисс 7 отрезков длиной 10. На них, как на основаниях, строим прямоугольники, высоты которых соответственно равны 1, 1, 5, 7, 7, 3, 1. Полученная ступенчатая фигура и является искомой гистограммой.