Растворы.

Тема 2. Приложения химической термодинамики.

Теоретический материал, необходимый для выполнения самостоятельной работы по теме «Растворы»:

1) Способы выражения концентрации растворов.

2) Классификация растворов. Законы Дальтона, Рауля, Генри.

3) Термодинамика растворов.

4) Парциальные мольные величины и методы их определения.

5) Коллигативные свойства растворов. Растворимость.

 

Состав растворов обычно выражают в массовых процентах (или в массовых долях), в молях растворенного вещества на 1л раствора (молярность) или на 1 кг растворителя (моляльность), а также в мольных долях. Формулы для расчета различных концентраций приведены в таблице (повторите и запомните их).

Массовая доля wi – отношение массы данного компонента раствора к массе раствора(gi – количество i-того вещества в г)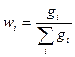
Массовое содержание рi (процентная концентрация) – масса растворенного i-того вещества (г) в 100 г раствора
Мольная доля хi – число молей растворенного вещества ni в 1 моле раствора
Молярность Сi– количество i-того компонента (в молях) в 1л раствора
Моляльность mi – количество i-того компонента (в молях) в 1000 г растворителя

 

Для пересчета концентраций можно использовать следующие соотношения (индекс 1 относится к растворителю, 2 – к растворенному веществу, M_i – молекулярная масса, г/моль; ρ – плотность раствора, г/см³):

, ;

, ;

, .

Среднюю молекулярную массу раствора рассчитывают по формуле:

(17)

Согласно закону Дальтона парциальное давление p_i газа в смеси пропорционально общему давлению Р и мольной доле этого газа в газовой фазе х_i:

р_i = Px_i . (18)

В соответствии с законом Рауля для бинарного раствора:

, (19)

т. е. относительное понижение давления пара растворителя над раствором равно мольной доле растворенного вещества.

Если оба компонента летучи, то закон Рауля выполняется для каждого из компонентов идеального раствора на всем интервале составов, а общее давление пара над раствором равно сумме парциальных давлений компонентов и линейно зависит от состава раствора:

, (20)

. (21)

Уравнение Рауля, учитывающее диссоциацию растворенного вещества в растворе, имеет вид:

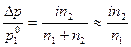, (22)

где , а i – изотонический коэффициент Вант-Гоффа:

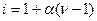, (23)

α – степень диссоциации вещества в растворе, ν – число ионов, на которые распадается молекула.

В предельно разбавленных растворах для растворителя выполняется закон Рауля, а для растворенного вещества – закон Генри:

, (24)

где К_Г – константа Генри. В идеальных растворах закон Генри совпадает с законом Рауля ( ).

Для описания свойств реальных растворов вводится понятие термодинамической активности а_i компонента в растворе – эффективной (или реально действующей) концентрации данного вещества с учетом взаимодействий между частицами в растворе. Поправочным коэффициентом, учитывающим все виды взаимодействия в реальном растворе, служит коэффициент активности γ_i:

, (25)

где абсолютная величина активности и коэффициента активности зависит от способа выражения концентрации раствора.

 

Активность можно рассчитать из уравнения для химического потенциала:

, (26)

где 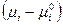- разность химических потенциалов вещества в данной фазе и в стандартном состоянии при одних и тех же Р и Т, а также определить через экспериментально измеряемые величины парциальных давлений:

(27)

или фугитивностей (летучестей):

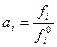. (28)

Коэффициенты активности растворителя и растворенных веществ могут быть рассчитаны на основании отклонений от законов Рауля и Генри соответственно:

, (29)

. (30)

Вклад компонента в любое общее экстенсивное свойство Ф раствора определяется его парциальной мольной величиной, которая выражается как частная производная от любой экстенсивной переменной Ф по количеству i-того компонента (в молях) при постоянных давлении, температуре и числе молей остальных компонентов системы:

. (31)

Парциальная мольная величина отражает изменение какого-либо экстенсивного свойства раствора Ф при изменении количества i-того компонента на dn_i в условиях постоянства Р,Т и состава раствора в расчете на 1 моль.

Особенности парциальных величин:

- характеризуют не само свойство, а его изменение, поэтому в отличие от мольных величин ( ) они могут принимать любые значения (положительные, отрицательные, нулевые и даже бесконечные);

- парциальные мольные величины зависят от состава раствора, поэтому при определении численного значения парциальной величины необходимо указывать состав;

- парциальные мольные величины различных компонентов раствора зависят друг от друга и связаны уравнением Гиббса-Дюгема:

, (32)

которое позволяет по известной зависимости парциальной мольной величины одного компонента от состава рассчитывать парциальные мольные величины других компонентов и далее – интегральные свойства системы.

Парциальными молярными величинами могут быть объем , энтальпия , энтропия , теплоемкость , энергия Гиббса и Гельмгольца . По определению парциальная мольная энергия Гиббса тождественна химическому потенциалу:

. (33)

Общее (интегральное) значение свойства раствора представляет собой сумму вкладов всех компонентов раствора с учетом их количества (свойство аддитивности парциальных мольных величин):

. (34)

Для бинарного раствора свойство аддитивности запишется следующим образом:

, (35)

а в расчете на 1 моль раствора:

, (36)

где - мольная величина, т. е. свойство одного моля раствора, может быть определена соотношением

. (37)

Энергия Гиббса двухкомпонентного раствора, отнесенная к 1 молю:

. (38)

. (39)

Величину ∆G в уравнении (39) называют энергией Гиббса образования раствора. Если раствор и его компоненты имеют одну и ту же структуру (общепринятый выбор стандартного состояния компонентов в растворе), то функции образования совпадают с функциями смешения (∆Ф^mix, где Ф = G, H, S, V). Интегральные функции смешения рассчитывают по формулам (35, 36), а парциальные мольные функции смешения определяют как:

, (40)

где - экстенсивная функция Ф i-того компонента в стандартном состоянии.

Так парциальная энергия Гиббса смешения в идеальном растворе:

, (41)

а парциальная мольная энтропия смешения:

. (42)

Изменение объема и тепловой эффект в случае идеальных растворов отсутствуют ( , ).

Методы определения парциальных свойств:

• Аналитический – дифференцирование аналитической зависимости интегрального свойства от состава раствора по количеству молей одного из компонентов.

Если зависимость Ф=f(n₂) может быть аппроксимирована полиномом :

,

то парциальная мольная характеристика растворенного вещества определяется как

,

а парциальная мольная характеристика растворителя может быть рассчитана на основании свойства аддитивности (35):

.

• Графические – основаны на построении касательных к зависимости свойство раствора – состав, причем состав раствора может быть выражен через число молей одного из компонентов, мольную или массовую долю:

а) к кривой Ф = f(n₂) → парциальное свойство (метод касательных),

б) к кривой Ф = f(х₂) или Ф = f(ω₂) →парциальные свойства 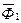и (метод пересечений).

 

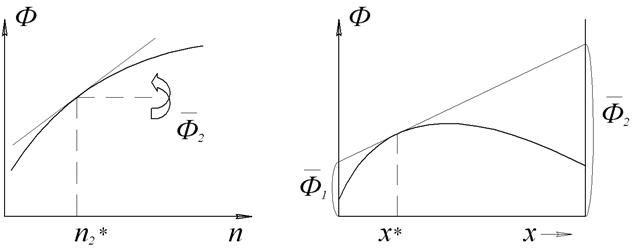
а) б)

Рис. 3 Графические методы определения парциальных мольных

величин на основании зависимости свойства раствора от состава:

а) от числа молей растворенного вещества n₂ – метод касательных;

б) от мольной доли растворенного вещества x₂ – метод пересечений.

 

Свойства разбавленных растворов, зависящие только от количества нелетучего растворенного вещества в единице объема раствора (но не от его природы), называются коллигативными. К ним относятся: понижение давления пара растворителя над раствором, повышение температуры кипения и понижение температуры замерзания раствора, а также осмотическое давление.

Понижение температуры замерзания ( 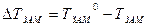) и повышение температуры кипения ( ) разбавленного раствора по сравнению с чистым растворителем:

, (43)

, (44)

где и – температуры замерзания и кипения чистого растворителя; М₁ – молярная масса растворителя; х₂ и m₂ – мольная доля и моляльность растворенного вещества; ∆H _пл и ∆H_кип – мольные энтальпии плавления и испарения растворителя; К_к и К_э – криоскопическая и эбуллиоскопическая постоянные растворителя; 1000 – поправочный коэффициент, учитывающий массу растворителя в растворе с моляльностью m₂ (g₁=1000 г).

По понижению температуры замерзания (повышению температуры кипения) раствора можно определить молекулярную массу растворенного вещества М₂ и установить наличие ассоциации или диссоциации частиц в растворе:

, (45)

, (46)

где g₁ и g₂ – массы растворителя и растворенного вещества в растворе, соответственно.

Осмотическое давление π в разбавленных растворах можно рассчитать по уравнению Вант-Гоффа:

, (47)

где С – молярная концентрация раствора.

Уравнения, описывающие коллигативные свойства растворов неэлектролитов, можно применять и для описания свойств растворов электролитов, введя поправочный коэффициент Вант-Гоффа i, определяемый по уравнению (23):

, (48)

, (49)

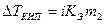. (50)

Растворимость твердого вещества в идеальном растворе при температуре Т описывается уравнением Шредера:

, (51)

где х₂, Т_ПЛ, ∆Н_ПЛ – мольная доля, температура плавления и молярная теплота плавления растворенного вещества.

Зависимость растворимости газов в жидкостях от давления описывается уравнением Генри (24) , где х₂ – мольная доля газа в насыщенном растворе, а зависимость растворимости газов от температуры - интегральным уравнением вида:

, (52)

где ∆Н_Р – дифференциальная теплота растворения газа в насыщенном растворе.

Растворение вещества в двух несмешивающихся друг с другом растворителях выражается законом распределения:

, (53)

где С₁ и С₂ – равновесные концентрации распределяющегося вещества в первом и втором растворителях, К – коэффициент распределения.

В реальных растворах концентрации в выражении закона распределения (53) следует заменять активностями.

При диссоциации (ассоциации) вещества в одном из растворителей используют уравнение Шилова-Лепиня:

, (54)

где n = M₂/M₁ , M₁ и M₂ – средняя молекулярная масса распределяющегося вещества в первом и втором растворителях.

В случае если степень диссоциации α растворенного вещества в растворителях 1 и 2 различна, то уравнение (53) преобразуется к виду:

. (55)

Закон распределения применяется для описания процесса экстракции. Масса вещества g, оставшегося в растворе после n-го шага экстрагирования может быть рассчитана по формуле:

, (56)

где g₀ – начальная масса экстрагируемого вещества в растворе, V – объем этого раствора, ν – объем порции экстрагента, n – число стадий экстракции.