Теорема Клини

Регулярные выражения — это конечные формулы, задающие регулярные языки. Но подобным же свойством обладают и конечные автоматы — они тоже задают языки. Возникает вопрос: как соотносятся между собой классы языков, задаваемые конечными автоматами и регулярными выражениями? Обозначим 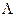_А множество автоматных языков, 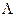_R — множество регулярных языков. Стефен Клини, американский математик, доказал следующую теорему.

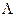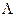Теорема 2.(Теорема Клини.) Классы регулярных множеств и автоматных языков совпадают, то есть _А = _R.

Иными словами, каждый автоматный язык может быть задан формулой (регулярным выражением) и каждое регулярное множество может быть распознано конечным автоматом. Мы докажем эту теорему конструктивно, в два шага. На первом шаге докажем, что любой автоматный язык является регулярным множеством (или, что то же, для любого конечного автомата можно построить регулярное выражение, задающее распознаваемый этим автоматом язык). На втором шаге докажем, что любое регулярное множество является автоматным языком (или, что то же, по любому регулярному выражению можно построить конечный автомат, допускающий в точности цепочки соответствующего регулярного множества).

Введем в рассмотрение модель графа переходов как обобщение модели конечного автомата. В графе переходов одна начальная и произвольное количество заключительных вершин, а направленные ребра помечены, в отличие от конечного автомата, не символами, а регулярными выражениями. Граф переходов допускает цепочку а, если апринадлежит множеству цепочек, описываемую произведением регулярных выражений R₁R₂...R_n, которые помечают путь из начальной вершины в одну из заключительных вершин. Множество цепочек, допускаемых графом переходов, образует допускаемый им язык.

Рис. 1. Граф переходов

На рис. 1 изображен граф переходов, который допускает, например, цепочку abbca, поскольку путь s->r—>p—>s—>r—>q, который ведет в заключительное состояние q, помечен цепочкой регулярных выражений e·a·b*·e·c*а. Конечный автомат является частным случаем графа переходов и поэтому все языки, которые допускаются автоматами, допускаются и графами переходов.

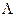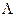Теорема 3.Каждый автоматный язык является регулярным множеством, _АÍ _R.

Доказательство. Граф переходов с одной начальной и одной заключительной вершинами, у которого единственное ребро из начальной в заключительную вершину помечено регулярным выражением R, допускает язык R^{^} (рис. 1).

Рис. 2. Граф переходов, допускающий регулярный язык FT

Докажем теперь, что каждый автоматный язык является регулярным множеством приведением любого графа переходов без изменения допускаемого им языка к эквивалентному виду (рис. 2).

Любой конечный автомат и любой граф переходов всегда можно представить в нормализованной форме, в которой только одна начальная вершина только с исходящими ребрами и только одна заключительная вершина только с входящими ребрами (рис. 3).

 

Рис. 3. Граф переходов с одной начальной и одной заключительной вершинами

С графом переходов, представленным в нормализованной форме, могут быть выполнены две операции редукции — редукция ребра и редукция вершины — с со­хранением допускаемого этим графом переходов языка:

а) редукция ребра:

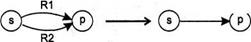
R1+R2

 

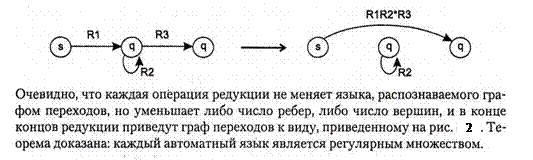б) редукция вершины (замена выполняется для каждого пути, проходящего через вершину р, с последующим ее выбрасыванием как недостижимого состояния):

Очевидно, что каждая операция редукции не меняет языка, распознаваемого графом переходов, но уменьшает либо число ребер, либо число вершин, и в конце концов редукции приведут граф переходов к виду, приведенному на рис. 2. Теорема доказана: каждый автоматный язык является регулярным множеством.

Пример

Пусть задан конечный автомат А:

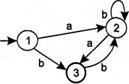
А::

 

Строим эквивалентный граф переходов в нормализованном виде.

Редукция вершины 3:

 

Редукция дуг и применение правила Re = R:

Редукция вершины 2:

Редукция дуги и вершины 1:

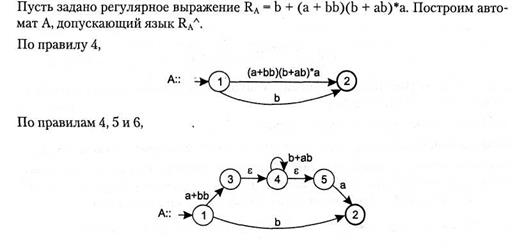
Таким образом язык, распознаваемый автоматом А, задается регулярным выраже­нием: R_A = b+(a+bb)(b+ab)*a.

Докажем теорему Клини в другую сторону.

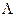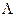Теорема 2.Каждое регулярное множество является автоматным языком: _RÍ _A.

Доказательство.Покажем, что для каждого регулярного выражения R может быть построен конечный автомат A_r (возможно, недетерминированный), распознающий язык, задаваемый R. Определение таких автоматов дадим рекурсивно.

(начальное и заключительное состояния А совмещаются).

Пример (продолжение)