Задача 5.5

Для определения средней заработной платы рабочих завода была произведена 20%-ная бесповторная выборка (по цехам) с отбором единиц пропорционально численности групп. Результаты выборки представлены в приводимой ниже таблице:

Цех	Объем выборки, чел., пi	Средняя заработная плата, руб.,	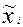Среднее квадратическое отклонение, руб., σi
Всего		—	—

С вероятностью 0,997 (т.е. t = 3) определить пределы, в которых находится средняя заработная плата всех рабочих завода.

Решение.

А. Находим общую выборочную среднюю заработную плату:

(руб.)

Б. Находим среднюю из групповых дисперсий:

.

В. Определяем предельную ошибку выборочной средней зара­ботной платы. Для типической бесповторной выборки

Отсюда генеральная средняя

или ,

т.е. средняя заработная плата всех рабочих находится в пределах от 880,5 руб. до 896,3 руб.

В статистике часто приходится сравнивать результаты двух (или более) выборок. И на основании сравнения двух выборочных сред­них (или долей) делается вывод о случайности или существенности их расхождений. Для этого абсолютная разность показателей сопоставляется со средней ошибкой разности . Если при п > 20 результат этого соотношения t< 3, то делается вывод о случайности расхождений. Если же объем вы­борки мал, т.е. п 20, то полученное значение t (фактическое) срав­нивают с табличным, определяемым по таблицам t-распределения Стьюдента при заданном числе степеней свободы и уровне значимо­сти. И если t_факт < t_табл , расхождения можно считать случайными. (Число степеней свободы при этом определяется как п₁ + п₂ — 2.)