Формулы для расчета основных показателей выборочного наблюдения

 

Наименование	Выборочное наблюдение
показателя	бесповторное	повторное
Численность выборки для средней	t²D N nx = (Dx)²N + t²D	t²D nx = (Dx)²
Численность выборки для доли	t²w(1-w) N nw = (Dw)²N + t²w(1-w)	t²w(1-w) nw = (Dw)²
Генеральная средняя
Генеральная доля	p = w ± Dw
Выборочная средняя	åxi fi x = åfi
Выборочная доля	m w = n
Предельная ошибка для средней
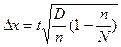
Предельная ошибка для доли

 

Для расчета объема выборки нужно знать дисперсию. Она может быть заимствована из проводимых ранее обследований данной или аналогичной совокупности, а если таковых нет, тогда для определения дисперсии надо провести специальное выборочное обследование небольшого объема.

Задача: Владелец автостоянки опасается обмана со стороны своих служащих (охраны автостоянки). В течение года (365 дней) владельцем автостоянки проведено 40 проверок. По данным проверок среднее число автомобилей, оставляемых на ночь на охрану, составило 400 единиц, а среднее квадратическое (стандартное) отклонение их числа – 10 автомобилей.

Считая отбор собственно-случайным, с вероятностью 0,99 оцените с помощью доверительного интервала истинное среднее число автомобилей, оставляемых на ночь на охрану. Обоснованы ли опасения владельца автостоянки, если среднее число автомобилей, оставляемых на ночь на охрану, составляет 395 единиц?

В 24 из 40 проверок число автомобилей на стоянке не превышало 400 единиц. С вероятностью 0,98 найдите доверительный интервал для оценки истинной доли дней в течение года, когда число оставляемых на стоянке автомобилей не превышало 400 единиц.

Каким должен быть объем выборки (число проверок), чтобы с вероятностью 0,95 можно было утверждать, что ошибка выборки для средней не превышает 3 автомобиля, если стандартное отклонение равно 10 автомобилям?

 

1. По условию задачи выборочное обследование проведено с помощью собственно-случайного отбора. Очевидно, что отбор бесповторный, так как не имеет смысла производить проверку более 1 раза в сутки.

Известно, что объем генеральной совокупности N=365 дней;

объем выборки п=40;

средняя выборочная =400 автомобилей;

среднее квадратическое отклонение =10 автомобилей;

вероятность Р=0,99.

Необходимо найти генеральную среднюю, выраженную в доверительном интервале по формуле: .

Предельная ошибка выборки для средней при бесповторном отборе находится по формуле:

автомобиля.

Коэффициент доверия t находится в зависимости от вероятности, в данном случае t=2,58. Дисперсия связана со стандартным отклонение следующим равенством: .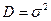

.

С уверенностью в 99% можно ожидать, что среднее число автомобилей, оставляемых на ночь на охрану находится в интервале от 396 до 404. Таким образом, можно утверждать, что служащие автостоянки обманывают ее владельца.

 

2. Известно, что объем генеральной совокупности N=365 дней;

объем выборки п=40;

число проверок, в которых число автомобилей на стоянке не превышало 400 единиц т=24;

вероятность Р=0,98.

Необходимо найти генеральную долю, выраженную в доверительном интервале по формуле: .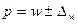

Выборочная доля определяется как и равна 0,6 (или 60%).

Предельная ошибка выборки для доли при бесповторном отборе находится по формуле:

.

Коэффициент доверия t находится в зависимости от вероятности, в данном случае t=2,33.

Генеральная доля:

С вероятностью 0,98 можно ожидать, что доля дней в течение года, когда число оставляемых на стоянке автомобилей не превышало 400 единиц, находится в интервале от 0,43 до 0,77 или от 157 до 281 дня.

 

3. Известно, что объем генеральной совокупности N=365 дней;

предельная ошибка выборки для средней =3 автомобиля;

среднее квадратическое отклонение =10 автомобилей;

вероятность Р=0,95.

Необходимо найти численность выборки для средней при собственно-случайном бесповторном отборе по формуле:

Коэффициент доверия t находится в зависимости от вероятности, в данном случае t=1,96.

Так как п – целое число, округлим полученный результат до большего целого, учитывая, что необходимо не превышать заданную ошибку. Следовательно, необходимо провести на менее 39 проверок.