Результаты выборочного наблюдения уровня заработной платы

 

Результат наблюдения Расчет показателей
уровень заработной платы, тыс. руб. числен­ность работни­ков средний уровень заработной платы в группе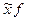
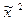
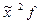
    f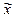            
До 9,0 8,5 68,0 72,25 578,00
9,0-10,0 9,5 209,0 90,25 1 985,50
10,0 –10,5 10,25 666,25 105,06 6 829,06
10,5–11,0 10,75 430,0 115,56 4 622,50
Свыше 11,0 11,25 168,75 126,56 1 898,44
Итого   1542,0 542,0   15 913,50

 

Для нахождения границ доверительного интервала необходимо определить предельную ошибку величины среднего уровня заработ­ной платы в выборочной совокупности.

Решение:

1) на основе выборочных данных определяем среднюю заработную плату обследованной совокупности рабочих (тыс. руб.):

2) определяем дисперсию признака в выборочной совокупности:

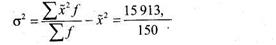– 105,678 = 0,41

3) в соответствии с формулами нахождения µ определяем величину средней ошибки µ (тыс. руб.):

 

4) коэффициент доверия находим по таблице, исходя из величины вероятности:

—в случае если Р = 0,683, t= 1,

—в случае если Р = 0,997, t = 3;

 

5) определяем величину предельной ошибки (тыс. руб.):

— в случае если t = 1, Δ = tµ = 1 * 0,052 = 0,052

(т.е. с вероятностью 0,683 величина генеральной средней не более чем на ±52 руб. будет отклоняться от выборочной средней),

 

— в случае если t = 3, Δ = tµ= 3 • 0,5212 = 0,156 ;

(т.е. с вероятностью 0,997 величина генеральной средней не более чем на ±156 руб. будет отклоняться от выборочной средней);

 

6) доверительные границы для среднего уровня заработной платы в генеральной совокупности составляют (тыс. руб.)

— с вероятностью 0,683: 10,28 – 0,052 ≤ 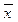≤10,28 + 0,052,
или 10,23 ≤ 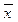≤10,33

(в 683 случаях из 1000 средний уровень заработной платы рабочих будет не ниже 10,23 тыс. руб. и не выше 10,33 тыс. руб.),

— с вероятностью 0,997: 10,28 - 0,15 ≤ 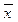≤ 10,28 + 0,156,
или 10,12 ≤ 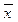≤10,44

(в 997 случаях из 1000 средний уровень заработной платы рабочих будет не ниже 10,12 тыс. руб. и не выше 10,44 тыс. руб.).

Таким образом, при заданной численности выборки повышение точности оценки генеральной средней (уменьшение границ довери­тельного интервала) приводит к уменьшению вероятности получения неточного результата, и наоборот, увеличение границ доверительного интервала, в котором находится генеральная средняя, — к повышению вероятности получения менее точного результата.