Алгоритмы решения задач выборочного метода
Тема «Выборочное наблюдение»
(тренировочные задания)
Задачи выборочного метода
1. Определение предельной ошибки выборки (или границ, в которых находится генеральная средняя (доля), на основе данных о численности и вероятности ошибки выборки.
2.Определение объема (численности) выборки, при котором пределы возможной ошибки не превысят некоторой наперед заданной величины с заданной вероятностью.
3. Определение вероятности того, что при наблюдении заданного числа единиц выборочной совокупности ошибка будет иметь заемный предел.
Алгоритмы решения задач выборочного метода
1. Определение величины предельной ошибки выборки.
Дано:
— способ отбора;
— численность выборки (n);
— вероятность ошибки выборки (Р);
— результаты выборочного наблюдения (распределение выборочной совокупности по изучаемому признаку).
Определить:предельную ошибку выборки для средней величины.
Решение:
1) по результатам выборочного наблюдения производится расчет среднего значения (доли) признака в выборочной совокупности — хср выб (ω);
2) определяется дисперсия признака в выборочной совокупности.
Расчет удобнее производить по формулам:
— для средней: 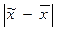
— для доли: 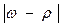
3) в соответствии с использованным способом отбора по формулам табл. 9.1 исчисляется величина средней ошибки выборки µ.
4) по таблице значений интеграла вероятностей нормального закона распределения в соответствии с заданной величиной вероятности ошибки выборки определяется величина коэффициента доверия t;
5) по формуле Δ = t µ, исчисляется величина предельной ошибки выборки — Δх (или Δω);
по формулам для средней: 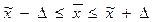 , или
, или
— для доли: 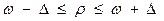
исчисляются границы, в которых находится величина генеральной средней (или генеральной доли).
Задача 1.На предприятиях города работает 15 000 рабочих определенной профессии. Необходимо провести обследование их месячной заработной платы и определить среднюю ее величину у одного рабочего данной профессии. Провести обследование всех рабочих не представляется возможным. По схеме случайного бесповторного отбора были получены данные о размере заработной платы 150 человек (табл. 9.2). Необходимо при заданном уровне доверия (вероятности) определить границы, в которых находится средний уровень заработной платы в генеральной совокупности.
По условию задачи известно, что отбор — случайный бесповторный;
N = 15 000;
п = 150.
Рассмотрим два варианта допустимой вероятности ошибки выборочного наблюдения — 0,683 и 0,997
Таблица 2