Объем случайной выборки
Доверительный интервал – это числовой интервал, который между верхней и нижней границами содержит с известной вероятностью значение параметра в генеральной совокупности.
Доверительный уровень – это математическое выражение нашей уверенности в том, что параметр генеральной совокупности находится в пределах доверительного интервала.
ДУ 95 % - существует 95% вероятность того, что интересующий нас параметр генеральной совокупности находится в пределах установленного в исследовании доверительного интервала.
Объем выборки определяется, исходя из доверительных интервалов и уровней.
Объем выборки при оценке долей.Если результаты опроса представляются в виде долей (процентов), для определения соответствующего объема выборки можно воспользоваться таблицей 3. Вся информация, содержащаяся в данной таблице, составлена на основе 95%-ного доверительного уровня. Для пользования этой таблицей нужно иметь некоторую оценку изучаемой доли. Для проведения исследований были разработаны три альтернативных вопроса, требующих ответа "согласен—не согласен". На первый из вопросов вы надеетесь получить утвердительный ответ 10% выборки, на второй — 20%, на третий — 85%. К тому же предположим, что требуется обеспечить узкий доверительный интервал, составляющий не более чем ±3% для каждого из трех вопросов в отдельности.
Таблица
Доверительные интервалы для различных объемов выборки и ожидаемой 1 доли (доверительный уровень равен 95%)
| Объем выборки, чел. | Ожидаемая доля | |||||||||
| 5% или 95% | 10% или 90% | 15% или 85% | 20% или 80% | 25% или 75% | 30% или 70% | 35% или 65% | 40% или 60% | 45% или 55% | 50% | |
| 4,4 | 6,0 | 7,1 | 8,0 | 8,7 | 9,2 | 9,2 | 9,5 | 9,8 | 10,0 | |
| 3,1 | 4,7 | 5,0 | 5,7 | 6,1 | 6,5 | 6,7 | 6,9 | 7,0 | 7,2 | |
| 2,5 | 3,5 | 4,2 | 4,6 | 5,0 | 5,3 | 5,5 | 5,7 | 5,7 | 5,8 | |
| 2,2 | 3,0 | 3,6 | 4,0 | 4,3 | 4,6 | 4,8 | 4,9 | 5,0 | 5,0 | |
| 1,9 | 3,0 | 3,2 | 3,6 | 3,9 | 4,1 | 4,3 | 4,4 | 4,5 | 4,5 | |
| 1,8 | 2,5 | 2,9 | 3,3 | 3,5 | 3,7 | 3,9 | 4,0 | 4,0 | 4,1 | |
| 1,6 | 2,3 | 2,7 | 3,0 | 3,3 | 3,5 | 3,6, | 3,7 | 3,8 | 3,8 | |
| 1,5 | 2,2 | 2,5 | 2,8 | 3,1 | 3,2 | 3,4 | 3,5 | 3,5 | 3,5 | |
| 1,4 | 2,0 | 2,4 | 2,7 | 2,9 | 3,1 | 3,2 | 3,3 | 3,3 | 3,3 | |
| 1,4 | 1,9 | 2,3 | 2,5 | 2,7 | 2,9 | 3,0 | 3,1 | 3,1 | 3,2 | |
| 1,1 | 1,5 | 1,8 | 2,0 | 2,2 | 2,4 | 2,5 | 2,5 | 2,6 | 2,6 | |
| 1,0 | 1,3 | 1,6 | 1,8 | 1,9 | 2,0 | 2,1 | 2,2 | 2,2 | 2,2 | |
| 0,8 | 1,1 | 1,3 | 1,5 | 1,6 | 1,7 | 1,7 | 1,8 | 1,8 | 1,8 | |
| 0,6 | 0,8 | 1,0 | 1,1 | 1,2 | 1,3 | 1,3 | 1,4 | 1,4 | 1,4 |
Из табл. 8.3 видно, что при доверительном интервале со значением не более чем ±3% при ожидаемой доле утвердительных ответов:
• 10% — объем выборки должен составлять 400;
• 20% — объем выборки должен составлять 700;
• 85% — объем выборки должен составлять около 600.
Таким образом, окончательный объем выборки при данных значениях должен составлять 700 человек (наибольший из трех требуемых объемов выборки).
Бывают случаи, когда необходимо задать другой доверительный уровень. Следовательно, примером, приведенным в табл. 8.3, руководствоваться нельзя. В этом случае объем выборки можно определить по формуле:

где z — z -балл, соответствующий требуемому доверительному уровню, а е — желаемый доверительный интервал. Z-баллы для различных доверительных уровней приведены в таблице.
Таблица
| Доверительный уровень, % | Z-балл |
| 2,57 | |
| 1,96 | |
| 1,64 |
Рассмотрим другую ситуацию, когда от группы респондентов необходимо получить ответ на вопрос: "Знакомы ли вы с рекламой тортов производства ОАО «Фабрика-кухня «Журавли»?, ожидая получить утвердительный ответ от 35% опрашиваемых. Кроме того, вам необходимо на 99% быть уверенными в том, что действительная доля положительных ответов будет находиться в пределах ±2%. Требуемый объем выборки при заданном доверительном уровне получается следующим образом:


Объем выборки велик, так как доверительный уровень и доверительный интервал задают высокий уровень точности. Однако объем выборки будет гораздо меньшим, если доверительный интервал возрастет до ±4%, а доверительный уровень снизится до 95%:



Рис. 8.2. Зависимость между объемом выборки и доверительным уровнем для трех значений ожидаемой ответной реакции при 95%-ном доверительном уровне
Табл. 8.3 также демонстрирует зависимость между доверительными интервалами и объемом выборки. Если полагать, что доверительный уровень имеет постоянную величину, то чтобы уменьшить доверительный интервал вдвое, объем выборки следует увеличить вчетверо. Например, при ожидаемой доле в 20% выборка из 100 участников обеспечивает доверительный интервал ±8%, выборка из 400 — ±4%, а выборка из 1600 участников — ±2%. Зависимость между точностью (выражающейся в меньших доверительных интервалах) и объемом выборки показана на рис. 8.2. Как видим, точность значительно увеличивается при небольшом увеличении объема выборки (приблизительно до 1000 участников), однако увеличение точности существенно замедляется, если объем выборки превышает 1000 участников. Вот почему при проведении большей части потребительских, маркетинговых и рекламных исследовательских работ выборка редко превышает 1000 участников.
Вычисление объема выборки в случае, когда оценивается среднее значение.Можно также определить объем выборки, если требуется оценить среднее значение в генеральной совокупности. В этих случаях, кроме указания доверительного уровня и доверительного интервала, необходимо располагать оценкой изменчивости изучаемого признака. (Мерой изменчивости переменной является среднеквадратическое (стандартное) отклонение. В главе 15 подробно рассматривается вычисление и интерпретация этой меры.) Поскольку значение среднеквадратического отклонения в генеральной совокупности редко бывает известно, его можно оценить одним из следующих трех способов.
1. Воспользуйтесь оценкой среднеквадратического отклонения на основании предыдущих аналогичных исследований, проведенных на той же генеральной совокупности.
2. Проведите небольшое пилотажное исследование; используйте среднеквадратическое отклонение, полученное в пилотажных исследованиях, в качестве оценки среднеквадратического отклонения в генеральной совокупности.
3. Вычислите сумму максимального и минимального значений изучаемой переменной и разделите ее на четыре.
Оценив среднеквадратическое отклонение и определив доверительный интервал и доверительный уровень, оценку объема Выборга можно получить по следующей формуле:

где так же, как и в предыдущей формуле, z представляет z-балл, соответствующий конкретному доверительному уровню (взят из приведенной ранее таблицы), а е — желаемый доверительный интервал. Новый член этой формулы, s, является оценкой среднеквадратического отклонения в генеральной совокупности.
Приводим пример, подобный только что рассмотренному. Представьте следующую ситуацию. Вы обратились к группе респондентов с просьбой: "Дайте, пожалуйста, оценку правдоподобия рекламы офисного оборудования фирмы Lanier по шкале от одного до пяти". Вы хотите на 95% быть уверенными в том, что истинное значение среднего рейтинга в генеральной совокупности будет находиться в пределах ±0,2 от среднего значения в выборке. Оценка среднеквадратического отклонения получена путем суммирования экстремальных значений шкалы и деления суммы на четыре, и равна 1,5 (т.е. 5 + 1 : 4 = 1,5). Необходимый объем выборки для заданного желаемого доверительного уровня будет равен 216. Рассчитывается он с помощью формулы:

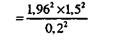


ГЛАВА 8. Выборка 249
Однако, несмотря на все преимущества, не всегда при проведении исследований в области рекламы используют случайную выборку. Для удовлетворения одних информационных потребностей не нужна точность и обобщаемость случайной выборки, а для удовлетворения других время и средства, затраченные на проведение случайной выборки, являются неоправданными. В этих случаях используется иная форма отбора — так называемая неслучайная выборка, при которой элементы выбираются некоторым неслучайным образом. Основными формами неслучайной выборки являются выборка первого встречного, выборка на основе экспертного суждения, квотная выборка и целенаправленная выборка.
Формы неслучайного отбора
Выборка первого встречного.Выборка первого встречного проводится именно так, как указано в ее названии: участники исследований отбираются в силу своей доступности и соображений удобства сбора данных. Опрос друзей, коллег по работе, просто случайных прохожих на улице — вот типичные примеры такой схемы отбора, так же, как и выбор последних тридцати сделок, которые находятся под рукой. Формирование выборки первого встречного, как и следовало ожидать, — несложный, недорогостоящий и быстро осуществимый процесс.
При формировании выборки первого встречного существует серьезная вероятность, что полученная информация будет совершенно ненадежной. Следовательно, использовать ее можно только в том случае, если нет абсолютно никакой необходимости обобщать отношение и поведение участников выборки первого встречного на более широкую генеральную совокупность. Поскольку нет никакой уверенности в том, что отличительные особенности участников выборки первого встречного репрезентативны для более широкой генеральной совокупности, использовать выборку первого встречного можно лишь при проведении предварительных пилотажных исследований или для получения быстрой информации необобщающего характера, отвечающей отдельным потребностям исследований, например предварительного тестирования анкеты.
Выборка на основе экспертного суждения.При проведении выборки на основе экспертного суждения участники выбираются из состава целевой совокупности, исходя из суждений эксперта о характерных особенностях репрезентативной выборки. В роли эксперта могут выступать сам исследователь, сотрудники рекламного агентства, клиент, специалист в конкретной предметной области. Например, владелец магазина может отобрать на основании собственных суждений "типичных" заказчиков.
Уверенность в результатах исследований, проводимых на основе экспертных суждений, прямо пропорционально зависит от опыта эксперта, на основании которого определяется и извлекается выборка. Чем больше опыт, тем выше вероятность получения достоверных результатов. Например, выбор городов для маркетингового тестирования нового товара почти всегда осуществляется на основе экспертных суждений. Лица, хорошо знающие товар и различные города Соединенных Штатов Америки, скорее всего, остановят свой выбор на более подходящих городах, в отличие от случайного выбора. С другой стороны, эксперт может полагать, что наиболее подходящей целевой аудиторией программы сбережений для поступления в колледж являются родители, имеющие детей от 10 до 17 лет. Если это суждение неверно, иссле-
Задания
1. Для каждой из следующих ситуаций определите соответствующую изучаемую совокупность и основу выборочного наблюдения.
a) Производитель нового вида сухих завтраков хочет провести домашнее тестирование продукта в Чикаго.
b) Национальная сеть магазинов хочет определить потребительские предпочтения покупателей, имеющих платежную карточку этой сети.
c) -Местная телевизионная станция хочет определить, какие передачи пользуются попу-
лярностью в семьях и каким именно программам зрители отдают предпочтение.
d) Местное отделение Американской ассоциации маркетинга хочет оценить эффективность работы своего нового представительства в Атланте.
2. Производитель хочет провести опрос потребителей, чтобы определить потенциальный спрос на новый пресс с механическим приводом. Новый пресс имеет мощность, равную 500 тонн и стоит 225 тысяч долларов. Он применяется для формовки изделий из легкой и тяжелой стали и полезен производителям автомобилей, строительного оборудования и крупных механических конструкций.
a) Определите генеральную совокупность и основу выборки, которые могут использоваться в данном случае.
b) Опишите, как получить простую случайную выборку, используя установленную вами основу выборки.
c) Можно ли провести стратифицированную выборку? Если да, то каким образом?
d) Можно ли применить кластерную выборку? Если да, то каким образом?
e) Какой из методов выборочного наблюдения вы порекомендуете? Почему?