Постановка задачи

 

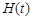Будем рассматривать объект управления, поведение которого описывает передаточная функция , а выходная переменная измеряется с помехой (см. рис. 6.2). Влияние окружающей среды отражает возмущение .

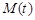Требования к поведению замкнутой системы заданы в виде оценок переходного процесса, в качестве которых используются статическая ошибка , перерегулирование ( ) и быстродействие ( ).

Необходимо определить передаточную функцию регулятора (корректирующего звена), включение которого в систему обеспечит в ней заданное качество работы.

Частотный метод синтеза предполагает использование асимптотических логарифмических амплитудных частотных характеристик, он применяется для расчета одноканальных систем, функционирующих в режиме слежения или отработки входного воздействия. Предполагается, что корректирующее звено (регулятор) на

ходится на входе системы. расчетная структурная схема системы имеет вид, изображенный на рис. 6.8.

Рассмотрим реакцию системы только на входное воздействие v, полагая возмущение и помеху равными нулю ( ), их влияние учтем в дальнейшем. Определим сначала передаточную функцию разомкнутой системы

, (6.27)

а затем замкнутой

(6.28)

Как видим, передаточную функцию замкнутой системы однозначно определяет .

Таким образом, если удастся сформировать определенную передаточную функцию или частотную характеристику для разомкнутой системы, то тем самым можно обеспечить требуемые свойства в замкнутой системе.

 

 

6.4.2. Влияние частотной характеристики
разомкнутой системы на свойства
замкнутой

 

Рассмотрим подробнее связь между частотными характеристиками разомкнутой и замкнутой систем, для чего от передаточной функции (6.27) перейдем к частотной характеристике

. (6.29)

Исследуем характеристику (6.29) в различных областях частот, как это принято в инженерной практике. введем предварительно несколько определений.

Зоной низких частот будем называть область изменения вблизи нуля. В ней по условию статики выполняется соотношение

где – коэффициент усиления объекта. Обычно поэтому для разомкнутой системы в соответствии с (6.29) получим

(6.30)

Областью высоких частот будем называть совокупность частот, намного превышающих полосу пропускания системы. Здесь справедливы соотношения

(6.31)

Под зоной средних частот будем понимать промежуток между зонами низких и высоких частот, где выполняются соотношения

(6.32)

Поскольку частотные характеристики разомкнутой и замкнутой систем связаны соотношением, аналогичным (6.28), с учетом (6.30) в области низких частот (НЧ) получим

т. е. частотная характеристика разомкнутой системы практически не влияет на аналогичную характеристику замкнутой системы.

В области высоких частот (ВЧ) с учетом (6.31) справедливо соотношение

а следовательно, частотная характеристика разомкнутой системы также не влияет на свойства замкнутой.

Таким образом, наибольшее влияние разомкнутая система оказывает на свойства замкнутой в области средних частот (СЧ), где необходимо наиболее тщательно формировать частотную характеристику .

 

 

6.4.3. Основные соотношения частотного
метода синтеза

 

На основе выражения (6.29) получим расчетные соотношения частотного метода синтеза. Если удается задать определенную частотную характеристику разомкнутой системы , то из (6.29) можно вычислить . Однако этот способ является громоздким и не нашел практического применения, но на его основе разработан удобный метод синтеза по ЛАЧХ. Запишем его расчетное соотношение, для чего частотную характеристику разомкнутой системы представим в форме

В соответствии с (6.29) для амплитудных частотных характеристик справедливо равенство

которое в логарифмическом масштабе принимает вид

(6.33)

Приравняв правую часть (6.33) , получим

Отсюда следует расчетное соотношение для логарифмической характеристики регулятора, которое является основным в частотном методе синтеза

(6.34)

Таким образом, для расчета регулятора необходимо построить логарифмическую амплитудную частотную характеристику (ЛАЧХ) объекта и на основе требований к качеству процессов в замкнутой системе сформировать ЛАЧХ разомкнутой системы. Затем следует определить ЛАЧХ регулятора в соответствии с выражением (6.34).