Гидравлический и пьезометрический уклоны
Как известно, энергия в природе не может ни теряться, ни возникатьиз ничего. Говоря о потерях энергии в потоке, имеют в виду ту часть механической энергии, которая из-за вязкости жидкости превращается в тепловую и через стенку трубопровода рассеивается в окружающую среду. Для природы в целом эта энергия не потеряна, но для потока она теряется необратимо, поскольку не может быть снова превращена в механическую энергию жидкости.
Причиной всех гидравлических потерь является вязкость жидкости, но далеко не всегда она оказывает существенное влияние на их величину. Потери удельной энергии или гидравлические потери зависят от формы потока, скорости течения и вязкости жидкости, а иногда и от абсолютного давления.
Гидравлические потери делятся на две группы - потери на трение по длине 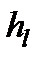 и местные потери
и местные потери 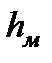 .
.
Потери на трение по длине – это потери, обусловленные действием внутреннего трения в жидкости и трением между ограничивающими поток стенками. Эти потери определяются по формуле Дарси-Вейсбаха
 , (3.28)
, (3.28)
где  - коэффициент трения по длине или коэффициент Дарси.
- коэффициент трения по длине или коэффициент Дарси.
Местные потери обусловлены местными сопротивлениями, вызывающими деформацию потока. Местные потери напора определяются по формуле Вейсбаха
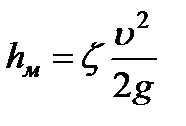 , (3.29)
, (3.29)
где 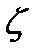 - безразмерный коэффициент, так называемый коэффициент местных потерь, или местных гидравлических сопротивлений.
- безразмерный коэффициент, так называемый коэффициент местных потерь, или местных гидравлических сопротивлений.
При протекании жидкости через местные сопротивления изменяется её направление и скорость, и возникают завихрения. Примерами местных сопротивлений могут служить сужения, расширения, повороты, дроссели, вентили, клапаны и другие устройства.
В гидравлических расчётах иногда удобно местные потери приводить к потерям по длине, оперируя фиктивной «эквивалентной длиной» трубопровода. Приравняв местные потери к потерям на эквивалентной длине потока, можно легко определить эту длину
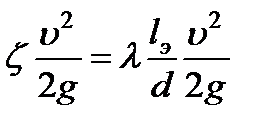 ,
,
откуда
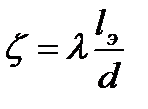 ,
,
или
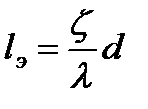 . (3.30)
. (3.30)
При таком подходе общие гидравлические потери в трубопроводе постоянного диаметра формально определяются как потери подлине
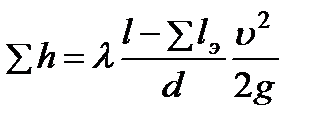 . (3.31)
. (3.31)
При решении многих задач технической гидродинамики потери удобнее определять через расход. Подставляя 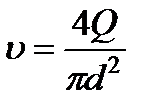 в формулы (3.28), (3.29) и (3.31), получим соответственно
в формулы (3.28), (3.29) и (3.31), получим соответственно
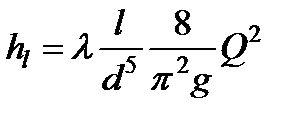 ; (3.32)
; (3.32)
 ; (3.33)
; (3.33)
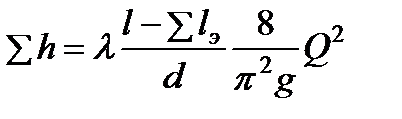 . (3.34)
. (3.34)
Если потери необходимо выражать в паскалях 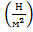 , то для этого достаточно умножить
, то для этого достаточно умножить 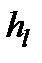 ,
, 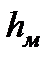 или
или 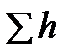 на удельный вес жидкости
на удельный вес жидкости 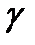 .
.
Откладывая последовательно потери и скоростной напор в виде соответствующих вертикальных отрезков вниз от линии полного напора для идеальной жидкости, получим напорную и пьезометрические линии для установившегося потока вязкой несжимаемой жидкости (рис. 3.13).
При построении такой диаграммы (или «эпюры трубопровода») местные потери рассматриваются как сосредоточенные, скачкообразные, поскольку участок возмущения, в пределах которого реализуется каждое из них, обычно мал по сравнению с общей протяжённостью потока. Что касается потерь по длине, то они уменьшают полный напор постепенно на протяжении всего трубопровода, определяя тем самым форму напорной линии.
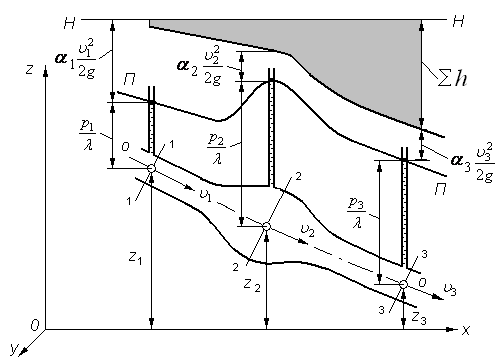
Рис. 3.13. Линии полных напоров Н-Н и пьезометрических
высот П-П для потока вязкой жидкости
Отношение потерь напора на цилиндрических участках трубопровода к соответствующей длине называют гидравлическим уклоном и обозначают буквой 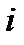 :
:
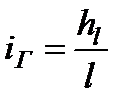 . (3.35)
. (3.35)
Гидравлический уклон – величина безразмерная и в общем случае переменная.
Понятие об уклоне можно ввести и для пьезометрической линии. Пьезометрическим уклоном называется изменение удельной потенциальной энергии жидкости, отнесённое к единице длины.
 . (3.36)
. (3.36)
Пьезометрический уклон может быть положительным, равным нулю и отрицательным (рис. 3.13).
На цилиндрических участках трубопровода напорная и пьезометрическая линии представляют собой параллельные прямые, поскольку расстояние между ними по вертикали равно постоянной величине 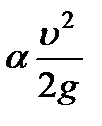 .
.