Решить симплексным методом, составить задачи ,двойственные данным, и найти их решения, используя теоремы двойственности.

Составить экономико-математическую модель.

Рацион для питания животных на ферме состоит из двух видов кормов I и II. Один килограмм корма I стоит 80 ден. ед. и содержит: 1 ед. жиров, 3 ед. белков, 2 ед. нитратов. Один килограмм корма II стоит 10 ден. ед. и содержит 3ед. жиров, 1 ед. белков, 8 ед. углеводов, 4 ед. нитратов.

Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 ед., белков не менее 9 ед., углеводов не менее 8 ед., нитратов не менее 16 ед.

Решить симплексным методом, составить задачи ,двойственные данным, и найти их решения, используя теоремы двойственности.

F = х₁+х₂ ® max

при ограничениях:

х₁ ≥ 0, x₂ ≥ 0.

 

7. Составить экономико-математическую модель.

На двух автоматических линиях выпускают аппараты трех типов. Другие условия задачи приведены в таблице.

 

Тип аппарата	Производительность работы линий, шт. в сутки	Затраты на работу линий, ден. ед. в сутки	План, шт.
А
В
С

 

Составить такой план загрузки станков, чтобы затраты были минимальными, а задание выполнено не более чем за 10 суток.

 

8. Решить симплексным методом, составить задачи ,двойственные данным, и найти их решения, используя теоремы двойственности.

Z = 10y₂ − 3y₃ ® min

при ограничениях:

у₁ ≥ 0, у₂ ≥ 0, у₃ ≥ 0.

 

9. Составить экономико-математическую модель.

Необходимо распилить 20 бревен длиной по 5 м каждое на бруски по 2 м и 3 м; при этом должно получиться равное количество брусков каждого размера.

Составить такой план распила, при котором будет получено максимальное число комплектов и все бревна будут распилены (в один комплект входит по одному бруску каждого размера).

 

10. Решить симплексным методом, составить задачи, двойственные данным, и найти их решения, используя теоремы двойственности.

Для производства двух видов изделий А и В предприятие использует три вида сырья. Другие условия задачи приведены в таблице.

 

Вид сырья	Нормы расхода сырья на одно изделие, кг	Общее количество сырья, кг
А	В
I
II
III
Прибыль от реализации одного изделия, ден. ед.

 

Составить такой план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной при условии, что изделий В надо выпустить не менее, чем изделий А.

 

11. Составить экономико-математическую модель.

Для производства двух видов изделий А и В предприятие использует три вида сырья. Другие условия задачи приведены в таблице.

 

Вид сырья	Нормы расхода сырья на одно изделие, кг	Общее количество сырья, кг
А	В
I
II
III
Прибыль от реализации одного изделия, ден. ед.

 

Составить такой план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной при условии, что изделий В надо выпустить не менее, чем изделий А.

 

12. Решить симплексным методом, составить задачи ,двойственные данным, и найти их решения, используя теоремы двойственности.

F = х₁+х₂ ® max

при ограничениях:

х₁ ≥ 0, x₂ ≥ 0.

 

13. Решить геометрически:

F = 3x₁+3x₂ → max

при ограничениях:

х₁ ≥ 0, x₂ ≥ 0; (IV,V)

 

14. Для изготовления четырех видов продукции (А, Б, В, Г) используются три вида ресурсов (I, II, III). Другие условия задачи представлены в таблице.

 

Ресурсы	Запас ресурсов ед.	Нормы расхода сырья на единицу продукции, ед.
А	Б	В	Г
I				0,5
II
III
Прибыль от единицы продукции, ден. ед.	7,5

 

Необходимо:1. Определить план выпуска продукции, при котором прибыль от ее реализации будет максимальной.

2. Сформулировать экономически, записать и решить двойственную задачу. Пояснить экономический смысл полученных объектов обусловленных оценок ресурсов.

3. Найти интервалы устойчивости двойственных оценок по отношению к изменению запаса ресурсов каждого вида.

4. Определить изменение максимальной прибыли от реализации продукции при увеличении запаса ресурса I на 40 ед., ресурса III на 50 ед. и уменьшении запаса ресурса II на 30 ед. Оценить раздельное влияние этих изменений и суммарное влияние.

5. Определить нормы заменяемости ресурсов.

6. Сопоставить оценку затрат и прибыли по оптимальному плану и каждому виду продукции.

7. Оценить целесообразность введения в план пятого вида продукции Д, нормы расхода сырья на единицу которого соответственно равны 2, 4, 2 ед., а прибыль – 15 ден. ед.

 

15. Решить геометрически:

F = 2x₁ − 3x₂+1 → min

при ограничениях:

 

16. Используя геометрическое решение двойственной задачи и теоремы двойственности, решите задачу линейного программирования.

F = - 4x₁ – 18x₂ – 30x₃ – 5x₄ → max

при ограничениях:

x_j ≥ 0, j = 1, 2, 3, 4.

 

17. Решить геометрически:

F = 2x₁ − 6x₂ → max

при ограничениях:

 

18. Методом Гомори (или методом ветвей и границ) найти оптимальное решение задач целочисленного линейного программирования. Дать геометрическую интерпретацию процесса решения задачи.

Z = 3x₁+2x₂ →max

при ограничениях:

х₁ ≥ 0, х₂ ≥ 0,

x₁, x₂ – целые числа

 

19. Решить геометрически:

F = 2x₁ − x₂ → min

при ограничениях:

x₁ ≥ 0, x₂ ≥ 0.

 

20. Методом Гомори (или методом ветвей и границ) найти оптимальное решение задач целочисленного линейного программирования. Дать геометрическую интерпретацию процесса решения задачи.

Z = 5x₁+7x₂ →min

при ограничениях:

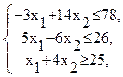
х₁ ≥ 0, х₂ ≥ 0,

x₁, x₂ – целые числа

 

21. Решить геометрически:

F = x₁+x₂ → max

при ограничениях:

x₁ ≥ 0, x₂ ≥ 0.

 

22. Методом Гомори (или методом ветвей и границ) найти оптимальное решение задач целочисленного линейного программирования. Дать геометрическую интерпретацию процесса решения задачи.

Z = 2x₁+x₂ → max

при ограничениях:

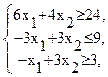
х₁ ≥ 0, х₂ ≥ 0,

x₁, x₂ – целые числа

 

23. Решить геометрически:

F = 2x₁ − x₂ → min

при ограничениях:

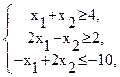
x₁ ≥ 0, x₂ ≥ 0.

 

24. Методом Гомори (или методом ветвей и границ) найти оптимальное решение задач целочисленного линейного программирования. Дать геометрическую интерпретацию процесса решения задачи.

Z = 6x₁+x₂ →min

при ограничениях:

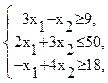
х₁ ≥ 0, х₂ ≥ 0,

x₁, x₂ – целые числа

 

25. Решить симплексным методом:

F = 2x₁ − 6x₂ → max

при ограничениях:

x₁ ≥ 0, x₂ ≥ 0.

 

26. Исследовать выпуклость следующих функций:

а) при х = 0;

б) ;

в)

г)

д) при х₁ > 0, х₂ >0.

 

27. Решить симплексным методом:

F = 2x₁ − x₂ → min

при ограничениях:

x₁ ≥ 0, x₂ ≥ 0.

 

28. Решить геометрически задачу выпуклого программирования:

 

29. Решить симплексным методом:

F = x₁+x₂ → max

при ограничениях:

x₁ ≥ 0, x₂ ≥ 0.

 

30. Решить методом кусочно-линейной аппроксимации:

Z = (x₁ – 3)² + 2(x₂ – 2)² → min

Указание:Отрезок изменения переменной х₁ [0;5] разбить на пять частей, а отрезок переменной х₂ [0;4] разбить на четыре части.

 

31. Решить симплексным методом:

F = 2x₁ − x₂ → min

при ограничениях:

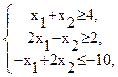
x₁ ≥ 0, x₂ ≥ 0.

 

32. Решить методом кусочно-линейной аппроксимации:

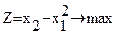
Указание:Отрезок изменения каждой из переменных разбить на четыре части.

 

33. Решить симплексным методом:

F = x₁ − x₂ → max

при ограничениях:

x₁ ≥ 0, x₂ ≥ 0.

 

34. Для данной функции найти Z = х₁х₂ найти:

а) общее выражение градиента функции ;

б) линию уровня, проходящую через точку А (4;1) и градиент (А), и изобразить их на чертеже;

в) производную по направлению l = (-1;-1).

 

35. Решить симплексным методом:

F = 4x₁ − 2x₂ → max

при ограничениях:

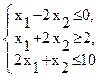
x₁ ≥ 0, x₂ ≥ 0.

 

36. Для данной функции найти Z = 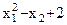найти:

а) общее выражение градиента функции ;

б) линию уровня, проходящую через точку А (4;1) и градиент (А), и изобразить их на чертеже;

в) производную по направлению l = (-1;-1).

 

37. Решить симплексным методом:

F = 2х₁ – 13х₂ – 6х₃ → max при ограничениях:

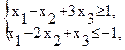
x₁ ≥ 0, х₂ ≥ 0, х₃ ≥ 0.

 

38. Найти оптимальное распределение средств между n предприятиями при условии, что прибыль f(x), полученная от каждого предприятия, является функцией от вложенных в него средств x. Вложения кратны , a функции f(x) заданы таблично.

 

x
f1(x)										s0 = 9,
f2(x)										n = 3,
f3(x)

 

s₀ = начальные средства ден. ед.

 

39. Решить симплексным методом:

F = - 6х₁+10х₂+9х₃+8х₄ → min при ограничениях:

x_j ≥ 0, j = 1, 2, 3, 4.

 

40. Найти оптимальное распределение средств между n предприятиями при услоage079-1202.gif"> f₂(x) f₃(x) f₄(x)

 

s₀ = начальные средства ден. ед.

 

45. Решить симплексным методом:

F = −4х₁+15х₂+12х₃+2х₄ → min при ограничениях:

x_j ≥ 0, j = 1, 2, 3, 4.

 

46. Найти оптимальное распределение средств между n предприятиями при условии, что прибыль f(x), полученная от каждого предприятия, является функцией от вложенных в него средств x. Вложения кратны , a функции f(x) заданы таблично.

 

x
f1(x)										s0 = 6, n = 3,
f2(x)
f3(x)
f4(x)

 

s₀ = начальные средства ден. ед.

 

47. Решить симплексным методом:

F = 14х₁+10х₂+14х₃+14х₄ → min при ограничениях:

x_j ≥ 0, j = 1, 2, 3, 4.

 

48. Найти оптимальное распределение средств между n предприятиями при условии, что прибыль f(x), полученная от каждого предприятия, является функцией от вложенных в него средств x. Вложения кратны , a функции f(x) заданы таблично.

 

x
f2(x)										s0 = 6, n = 3,
f3(x)
f4(x)

 

s₀ = начальные средства ден. ед.