Геометрическое определение вероятности.

Геометрической вероятностью события Аназывается отношение площади области D к площади области Ω (см. рис. 4), т.е. .

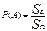Для случая, когда области D и Ωлинейные или объемные, вероятность вычисляется по формулам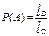

 

Пример 1. На отрезке длины 20 см помещен меньший отрезок длины 10 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадает также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

Решение. Пусть событие А - точка, поставленная в больший отрезок, попадет и в меньший отрезок. Следовательно, имеем по условию задачи длина большего отрезка =20 см и меньшего отрезка =10 см. Так как вероятность попадания точки на отрезок пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка , то вероятность попадания точки на отрезок определяется равенством .

 

Пример 2. В круг радиуса R вписан правильный треугольник. Найти вероятность того, что точка, брошенная в этот круг, попадет в данный треугольник.

Решение.Пусть область D – правильный треугольник, область Ω - круг радиуса R (см. рис. 5). Правильный треугольник, вписан в круг, следовательно, область D является частью области Ω. Событие А – точка, брошенная в круг. Так как вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга, то вероятность события А равна отношению площади области треугольника D к площади области круга Ω, т.е.

Выразим площадь треугольника АВС через радиус описанной окружности R(см. рис. 6). Так как треугольник АВС правильный то, следовательно, сторона треугольника вычисляется по формуле

-9 –

. Тогда площадь треугольника или площадь области D найдем по формуле

 

Пример 4.На отрезке ОА длины L числовой оси Ох наудачу поставлены две точки В(х) и С(у), причем у ≥ х. Найти вероятность того, что длина отрезка ВС меньше длины отрезка ОВ.

 

-10 -

 

Решение.Координаты точек В и С должны удовлетворять неравенствам 0 ≤ х ≤ L, 0 ≤ y ≤ L, у ≥ х как показано на рис.8. Введем в рассмотрение прямоугольную систему координат Оху. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей прямоугольному треугольнику ОКМ.

Таким образом, этот треугольник можно рассматривать как фигуру Ω, координаты точек которой представляют соответственно все возможные значения координат точек В и С.

Длина отрезка ВС должна быть меньше длины отрезка ОВ, т. е. Должно иметь место неравенство у – х < x, или y < 2x. Последнее неравенство выполняется для координат тех точек фигуры Ω (прямоугольного треугольника ОКМ), которые лежат ниже прямой у=2х (прямая ON). Как видно из рисунка все эти точки принадлежат заштрихованному треугольнику ONM. Таким образом, этот треугольник можно рассматривать как фигуру D, координаты точек которой являются благоприятствующими интересующему нас событию А - длина отрезка ВС меньше отрезка ОВ.

Найдем площадь треугольника ONM (см. рис.9): . Так как площадь треугольника OKM равна , а площадь треугольника . Следовательно, Искомая вероятность

 

 

-11 –