Статистическое и классическое определение вероятности
Классической вероятностью события А называется отношение числа т случаев благоприятствующих этому событию, к общему числу n случаев, т. е.
.
Статистической вероятностьюсобытия А называется число, около которого колеблется относительная частота события А при достаточно большом числе испытаний (опытов).
Предполагается, что элементарные исходы образуют полную группу и равновозможны.
Пример 1. В урне (емкости) находятся 12 белых и 8 черных шаров. Какова вероятность того, что наудачу вынутый шар будет белым?
Решение. Пусть А — событие, состоящее в том, что вынут белый шар. Ясно, что n = 12 + 8 = 20 — число всех равновозможных случаев (исходов опыта). Число случаев, благоприятствующих событию А, равно 12, т.е. т = 12. Следовательно, по формуле классического определения вероятности имеем: 
, т.е. Р(А)= 0,6.
Пример 2. Найти вероятность того, что в наудачу написанном двухзначном числе все цифры разные.
Решение. Пусть A – событие, состоящее в том, что написанное двухзначное число, имеет две разные цифры. Из 90 двухзначных чисел (от 10 до 99) 9 из них имеют одинаковые числа – это числа 11, 22, 33, 44, 55, 66, 77, 88, 99.
- 5 -
Тогда общее количество равновозможных случаев n = 90, а количество благоприятствующих для данного события m = 90 – 9 = 81. По формуле классического определения вероятности получаем 
, т. е. P(A) = 0,9.
Пример 3. В почтовом отделении имеются открытки 6 видов. Какова вероятность того, что среди 4 проданных открыток все открытки: а) одинаковы, б) различны.
Решение. Общее количество равновозможных исходов n, будем вычислять, используя формулу комбинаторики – сочетания с повторением. Выбрать 4 открытки из 6 видов можно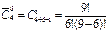 
=84 способами, т. е. n = 84.
а) Пусть событие A – состоит в том, что продано 4 одинаковые открытки. Число m исходов благоприятствующих наступлению события A, равно числу видов открыток m = 6. Тогда по формуле классического определения вероятности 
.
б) Пусть событие B – состоит в том, что проданы 4 различные открытки. Выбрать 4 открытки из 6 можно 
=15 способами, т. е. m=15. Следовательно, по формуле получаем 
Пример 4. В коробке 5 синих, 4 красных и 3 зеленных
карандаша. Наудачу вынимают 3 карандаша. Какова вероятность того, что среди них 2 синих и 1 зеленый карандаш?
Решение.Сначала найдем общее число способов выбора 3 карандашей из 12, имеющихся в наличии. Это и будет число благоприятствующих случаев. Сделаем это с помощью формулы сочетания без повторений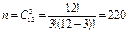 
.
Пусть событие А – из трех выбранных карандашей, 2 синих и 1 зеленый. Выбрать 2 синих карандаша из имеющихся 5 синих, можно сочетанием 2 из 5, то есть 
способами, а 1 зеленый из имеющихся 3 зеленых - 
способами.
- 6 –
Отсюда по правилу умножения получаем = 
10∙3=30. Тогда, по формуле классического определения вероятности 
.
Пример 5. Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту, появления бракованных книг.
Решение.Относительная частота события А – появление бракованных книг, равна отношению числа испытаний, в которых появилось событие А, к общему числу произведенных испытаний: n=100 – общее число произведенных событий, 
=5 – число событий, в которых появилось событие А. Тогда 