профиль подготовки «Менеджмент организации»

Контрольная работа по теме: «Множества»

 

Контрольная работа выполняется на двойных листах в клетку. В первой строке титульной страницы записывается:

Контрольная работа по теме: «Множества»

Студента (ки) I курса группы 10_ М

ФГБОУ ВПО «ВГАФК»

ФИО

Вариант (соответствует номеру в журнале преподавателя)

Работа выполняется в произвольном порядке (следует начинать с самого простого для Вас задания). Условие записывается полностью, графические работы и круги Эйлера выполняются только карандашом с использованием чертежных принадлежностей.

Работу следует сдать преподавателю сразу по окончании занятия. Задания, которые не были выполнены, являются домашним заданием и должны быть сданы преподавателю на ближайшем аудиторном занятии (лекции). Материалы работы размещены в сети в папке Бакалавриат и далее ФОС → Контрольные работы и СРС.

Контрольная работа по теме: «Множества»

Для студентов I курса направления подготовки 080200.62 «Менеджмент»

профиль подготовки «Менеджмент организации»

Задание 1. Составить список элементов множеств, заданных посредством характеристического признака:

 

№ варианта	Множество	№ варианта	Множество
	A = {х | х Î Z, -4,2 < х £ 3}		A = {х | х Î N, -6 < х < 6,7}
	A = {х | х Î N, -1,3 < х £ 6}		A = {х | х Î Z, -4 < х £ 4,6}
	A = {х | х Î Z, -5,4 £ х < 1}		A = {х | х Î N, -1 < х £ 7,5}
	A = {х | х Î N, -1 < х £ 6,1}		A = {х | х Î Z, -5 £ х < 2}
	A = {х | х Î Z, -2,6 £ х £ 1}		A = {х | х Î N, -1,8 < х £ 2,9}
	A = {х | х Î N, -7,3 £ х £ 2}		A = {х | х Î Z, -2 £ х £ 3,8}
	A = {х | х Î Z, -5,7 < х < 4}		A = {х | х Î N, -5,3 £ х £ 4}
	A = {х | х Î N, -3 < х < 2,7}		A = {х | х Î Z, -7 < х < 2}
	A = {х | х Î Z, -3,8 < х £ 3,3}		A = {х | х Î N, -8 < х < 6,1}
	A = {х | х Î N, -6,9 < х £ 5}		A = {х | х Î Z, -2,5 < х £ 6}
	A = {х | х Î Z, -2,5 £ х < 4,9}		A = {х | х Î N, -9 < х £ 2,2}
	A = {х | х Î N, -2 < х £ 5,2}		A = {х | х Î Z, -5 £ х < 3}
	A = {х | х Î Z, -3 £ х £ 4,7}		A = {х | х Î N, -8,6 < х £ 5,3}
	A = {х | х Î N, -8 £ х £ 5,3}		A = {х | х Î Z, -4,6 £ х £ 1}
	A = {х | х Î Z, -6 < х < 2,4}		A = {х | х Î N, -8 £ х £ 6,2}

 

Задание 2. Изобразить графически элементы множества, заданного посредством характеристического признака:

 

№ варианта	Множество	№ варианта	Множество
	B = {х |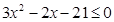}		B = {х |}
	B = {х |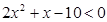}		B = {х |}
	B = {х |}		B = {х |}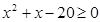
	B = {х |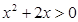}		B = {х |}
	B = {х |}		B = {х |}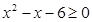
	B = {х |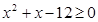}		B = {х |}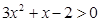
	B = {х |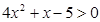}		B = {х |}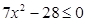
	B = {х |}		B = {х |}
	B = {х |}		B = {х |}
	B = {х |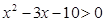}		B = {х |}
	B = {х |}		B = {х |}
	B = {х |}		B = {х |}
	B = {х |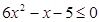}		B = {х |}
	B = {х |}		B = {х |}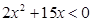
	B = {х |}		B = {х |}

 

Задание 3. Ответить на вопрос

 

№ варианта	Задание
	Привести пример таких множеств А и В, что А U В = Ø
	Привести пример таких множеств А и В, что m(А Δ В) = m(А U В)
	Привести пример таких множеств А, В, и С, что А Ì В, В Ì С и А Ì С.
	Привести пример таких множеств А и В, что одновременно А Ì В и А É В.
	Привести пример таких множеств А, В, и С, что А Ì В, В Ì С и А É С.
	Привести пример таких множеств А, В, и С, что А Ì В, В É С и А Ì С.
	Привести пример таких множеств А и В, что А U В = А ∩ В.
	Привести пример таких множеств А, В, и С, что А ∩ В = С.
	Привести пример таких множеств А и В, что А \ В = В \ А.
	Привести пример таких множеств А, В, и С, что А \ В = С.
	Привести пример таких множеств А, В, и С, что А Δ В = С.
	Привести пример таких множеств А и В, что А \ В = А ∩ В.
	Привести пример таких множеств А, В, и С, что А ∩ В = С.
	Привести пример таких множеств А и В, что А \ В = А U В.
	Привести пример таких множеств А и В, что А \ В = Ø.
	Привести пример таких множеств А и В, что А Δ В = Ø.
	Привести пример таких множеств А и В, что А ∩ В = Ø.
	Привести пример таких множеств А и В, что А ∩ В = А.
	Привести пример таких множеств А и В, что А \ В = А.
	Привести пример таких множеств А и В, что А U В = А.
	Привести пример таких множеств А и В, что А Δ В = А.
	Привести пример таких множеств А и В, что А \ В = А Δ В.
	Привести пример таких множеств А и В, что m(А \ В) = 2
	Привести пример таких множеств А и В, что m(А ∩ В) = 3
	Привести пример таких множеств А и В, что m(А U В) = 4
	Привести пример таких множеств А и В, что m(А Δ В) = 5
	Привести пример таких множеств А и В, что m(А \ В) = m(В \ A)
	Привести пример таких множеств А и В, что m(А ∩ В) = m(А \ В)
	Привести пример таких множеств А и В, что m(А U В) = m(А \ В)
	Привести пример таких множеств А и В, что m(А Δ В) = m(А \ В)

 

Задание 4. Найти объединение, пересечение, разность и симметрическую разность множеств А и В, если

№ варианта	Множество	№ варианта	Множество
	А={1, 2, 3, 4, 5}, В={2, 4, 6, 8, 10}		А={a, f, k}, В={a, b, c, d, e, f, k }
	А={а, б, в, г, д, е}, В={а, в, д, к, и}		А={5, 7, 10}, В={5, 6, 7, 8, 9, 10}
	А={3, 4, 5}, В={2, 3, 4, 5, 6}		А={c, e, f}, В={a, d, c, f, k }
	А={а, б, в, г, д}, В={и, к, с}		А={4, 5, 6}, В={2, 4, 5, 6, 8, 10}
	А={ 2, 4, 6, 8, 10}, В={1, 3, 5}		А={г, д, е, и, п, р}, В={а, в, и}
	А={x, y, z}, В={a, b, c, x, y}		А={3, 6, 7}, В={2, 3, 4, 5, 6, 7}
	А={8, 9, 10}, В={5, 6, 7, 8, 9}		А={ г, д}, В={е, ж, з, с, т, ф, ч}
	А={d, e, f, k}, В={a, b, c, d, e, f, k }		А={ 3, 6, 9}, В={1, 2, 3, 4, 5, 6}
	А={7, 9, 10}, В={5, 6, 7, 8, 9, 10}		А={1, 2, 3, 4, 5}, В={2, 3, 4, 5, 6}
	А={d, e, f}, В={a, b, c, f, k }		А={а, б, в, г, д, е}, В={а, в, д}
	А={3, 4, 5}, В={2, 4, 5, 6, 8, 10}		А={3, 4, 5, 6}, В={2, 3, 4, 5, 6, 7}
	А={г, д, е, ;ж, з, и}, В={а, в, и}		А={а, б, в}, В={а, б, и, к, с}
	А={4, 5, 7}, В={2, 3, 4, 5, 6, 7}		А={ 2, 4, 6, 8}, В={1, 5, 9, 13, 17}
	А={ г, д}, В={и, к, с, т, ф, ч}		А={x, y}, В={a, b, c, x, y, z}
	А={2, 4, 6}, В={1, 2, 3, 4, 5, 6}		А={7, 8, 9, 10}, В={5, 6, 7, 8, 10}

Задание 5. Найти объединение, пересечение, разность и симметрическую разность множеств А и В, и изобразить графически, если

№ варианта	Множество	№ варианта	Множество
	А={а½аÎ(-7; 1]}, В={b½bÎ[-3;4]}		А={а½аÎ(-5; 1)}, В={b½bÎ(3;6)}
	А={а½аÎ[-6; 0]}, В={b½bÎ(-2;3]}		А={а½аÎ(-2; 6]}, В={b½bÎ[0;5]}
	А={а½аÎ(-3; 2)}, В={b½bÎ[-4;1]}		А={а½аÎ[-1; 4]}, В={b½bÎ[-2;5]}
	А={а½аÎ[-2; 0)}, В={b½bÎ(2;5]}		А={а½аÎ(-1; 3)}, В={b½bÎ(4;7]}
	А={а½аÎ(-6; 4]}, В={b½bÎ(-5;0]}		А={а½аÎ[-8; 4)}, В={b½bÎ(0;6]}
	А={а½аÎ(-4; 0)}, В={b½bÎ(1;7]}		А={а½аÎ(-9; 2]}, В={b½bÎ(-5;5]}
	А={а½аÎ[-6; 3)}, В={b½bÎ[-2;1]}		А={а½аÎ[-3; 3]}, В={b½bÎ(-2;0)}
	А={а½аÎ[-5; 7]}, В={b½bÎ(-4;0)}		А={а½аÎ[-9;5)}, В={b½bÎ[-4;0]}
	А={а½аÎ(-8; 0]}, В={b½bÎ[-7;-3)}		А={а½аÎ[-5; 1]}, В={b½bÎ(3;5]}
	А={а½аÎ[-7; 4]}, В={b½bÎ[5;7]}		А={а½аÎ(-4; 3]}, В={b½bÎ[-2;5)}
	А={а½аÎ[-8; -3)}, В={b½bÎ(-1;4)}		А={а½аÎ[-1; 7)}, В={b½bÎ(-3;5)}
	А={а½аÎ(-4; 2)}, В={b½bÎ[-2;7)}		А={а½аÎ(-5; 2)}, В={b½bÎ[3;7]}
	А={а½аÎ(-4; 4]}, В={b½bÎ(-3;2)}		А={а½аÎ[-7; 4]}, В={b½bÎ[-2;3)}
	А={а½аÎ[-4; 2]}, В={b½bÎ[-5;3)}		А={а½аÎ(-6; 2]}, В={b½bÎ(-3;6)}
	А={а½аÎ[-1; 4)}, В={b½bÎ[5;10]}		А={а½аÎ(-1; 1)}, В={b½bÎ[5;8)}

 

Задание 6. Задайте три пересекающихся числовых множества А, В и С такие, что m(А) = 3, m(В) = 4, m(С) = 5 Найти множества, которые будут получены в результате выполнения следующих операций и изобразить при помощи кругов Эйлера:

а) (АÈС)DВ; б) (АÇС)\В; в) С\BDА; г) АÇBÇC; д) В\(АÇС); е) (BDC)ÈA.

 

Задание 7. Решить задачу:

На первом курсе по направлению «Менеджмент» обучается а студентов. Из них b занимаются в драмкружке, c – поют в хоре, d – увлекаются спортом. В драмкружке e студентов из хора, в хоре k – спортсменов, в драмкружке n спортсменов; m спортсменов посещают и драмкружок и хор. Найти:

1. Сколько студентов не поют в хоре, не увлекаются спортом и не занимаются в драмкружке?

2. Сколько человек, занимающихся в драмкружке и в хоре, не занимаются спортом?

3. Сколько спортсменов драмкружка