Б) хотя бы одно отделение получит газеты с опозданием.

Решение: Введем события

А1 = (газеты доставлены своевременно в первое отделение),

А2 = (газеты доставлены своевременно во второе отделение),

А3 = (газеты доставлены своевременно в третье отделение),

по условию P(A1)=0,95; P(A2) = 0,9; P(A3)=0,8.

Найдем вероятность события Х = (только одно отделение получит газеты вовремя). Событие Х произойдет, если

или газеты доставлены своевременно в 1 отделение, и доставлены не вовремя во 2 и 3,

или газеты доставлены своевременно в 2 отделение, и доставлены не вовремя во 1 и 3,

или газеты доставлены своевременно в 3 отделение, и доставлены не вовремя во 2 и 1.

Таким образом,

Так как события А1, А2, А3 - независимые, по теоремам сложения и умножения получаем

Найдем вероятность события У=(хотя бы одно отделение получит газеты с опозданием). Введем противоположное событие = (все отделения получат газеты вовремя). Вероятность этого события

Тогда вероятность события У:

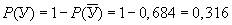
Ответ: 0,032; 0,316.

№21. В двух коробках лежат карандаши одинаковой величины и формы, но разного цвета. В первой коробке 4 красных и 6 черных, а во второй 3 красных, 5 синих и 2 черных. Из обеих коробок вынимается наугад по одному карандашу. Какова вероятность того, Что оба карандаша окажутся красными?

Решение. Испытание состоит в том, что из каждой коробки '' вынимается по одному карандашу. Пусть событие Аозначает, что вынутый карандаш из первой коробки оказался красным, событие

В— что вынутый карандаш из второй коробки тоже красный. Тогда событие АВозначает, что оба вынутые карандаша оказались красными. Поскольку события А и Внезависимы, то P (АВ) = P (А) P (В). Вероятности событий А и Вравны соответственно P(А) = 0,4, P(В) = 0,3. Следовательно, вероятность того, что оба карандаша оказались красными, равна P (АВ) =

=0,4 • 0,3 = 0,12.

Ответ: 0,12.

№22. В случайном эксперименте монету бросают трижды. Найти вероятность того, что орел не выпадет ни разу.

Решение: Задачу можно решить, пользуясь классическим определением вероятности или теоремой о произведении вероятностей.

1 способ. Решим задачу, используя теорему о произведении вероятностей.

Орел не выпадет ни разу только в случае выпадения: решка, решка, решка. Вероятность выпадения решки в 1-ый раз =0,5 (1 из двух вариантов выпадения). Аналогично: вероятность выпадения решки во 2-ой раз=0,5. И в 3-ий раз тоже =0,5. Поскольку это вероятности зависимых событий, мы находим их произведение: 0,5*0,5*0,5=0,125.

Ответ: 0, 125.

2 способ.

Решение: Эту задачу так же можно решить двумя способами.

1 способ. Решим, используя теорему о произведении. При каком сочетании может выпасть сумма 8? Найдём все комбинации: 2 и 6, 3 и 5, 4 и 4, 5 и 3, 6 и 2. Всего 5 комбинаций. 1/6 - вероятность выпадения 2 при первом бросании, и такая же вероятность выпадения будет у каждой из цифр. Подсчитаем вероятность выпадения комбинации 2 и 6: 1/6*1/6=1/36 (применили произведение вероятностей). Такая же вероятность будет у каждой из оставшихся 4-х комбинаций, каждая из которых дает нужную сумму 8.

1/36+1/36+1/36+1/36+1/36=5/36≈ 0,14. (применили сложения вероятностей).

Ответ: 0,14.

2 способ.Найдем число возможных исходов, переберём все варианты бросков. В подобных задачах удобнее составлять таблицу. Составим таблицу для суммы двух костей. ( все варианты суммы, которые могут выпасть):

Всего исходов 36 (6 на 6). Благоприятных исходов 5 ( легко подсчитать в таблице). Вероятность того, что в сумме выпадет 8 очков, равна: 5/36≈0, 14.

Ответ: 0,14.

№24. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Решение: 1способ.Найдем число возможных исходов, перебрав все варианты бросков. Составим таблицу, т.к. при решении подобных задач это удобно.

1-й бросок 2-й бросок

орел орел

орел решка

решка орел

решка решка

Всего возможных исходов 4. Орел выпадет один раз во втором и третьем вариантах. То есть число благоприятных исходов 2. Вероятность того, что орел выпадет ровно один раз равна: 2/4=0,5.

Ответ: 0,5.