Задача об оптимальном назначении

Постановка задачи.
Сотрудники: Иванов, Петров, Семенов, Михайлов, Васильев, Сидоров работают на предприятии. Производительность труда сотрудников на каждой операции (с № 1 по № 6) представлена в таблице:

Таблица 2.2.

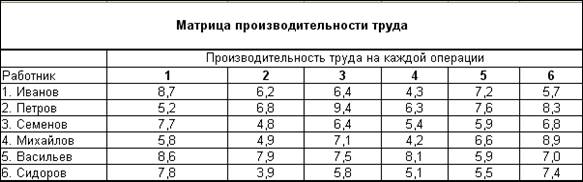
Распределить по должностям всех сотрудников так, чтобы суммарная производительность была максимальной.

Экономико-математическая модель. Данная задача является типичной моделью линейного целочисленного программирования (Ц.Л.П.), так как включает в себя двойственные ограничения на переменные (1- сотрудник назначается на должность, 0- сотрудник не назначается на должность).

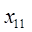– сотрудник 1.(Иванов) назначается на должность № 1;

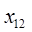– сотрудник 1.(Иванов) назначается на должность № 2;

………;

– сотрудник 1.(Иванов) назначается на должность № 6;

– сотрудник 2.(Петров) назначается на должность № 1;

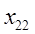– сотрудник 2.(Петров) назначается на должность № 2;

………;

………;

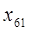– сотрудник 6.(Сидоров) назначается на должность № 1;

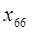– сотрудник 6.(Сидоров) назначается на должность № 6.

Имеем матрицу переменных:

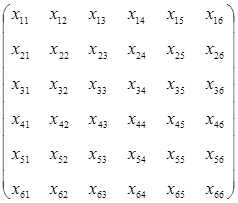
Целевая функция выражает суммарную производительность и имеет вид:

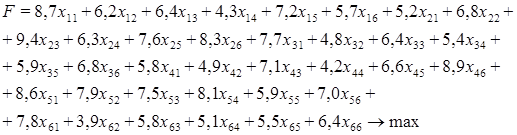
Ограничения:

Матрица переменных принимает двоичное значение:

1- сотрудник назначается на должность;

0- сотрудник не назначается на должность.

Табличная модель.

Рис. 2.9. Табличное представление модели

Рис. 2.10. Табличная модель с представленными формулами

Рис. 2.11. Диалоговое окно надстройки Поиск решения

Рис. 2.12.Решение задачи об оптимальном назначении

 

Задачки для самостоятельного решения ☺