ЗАДАЧИ по геометрии на карантин.
ГЕОМЕТРИЯ. ТРЕУГОЛЬНИКИ. ПОВТОРЕНИЕ.
| 1. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см на 1 см. Ответ дайте в квадратных сантиметрах. | 
| |
2. В треугольнике ABC угол С равен 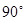 , , 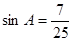 , найдите , найдите 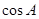 . .
| 
| |
| 3. Найдите площадь треугольника, вершины которого имеют координаты (1, 6), (9, 6), (9, 9). | 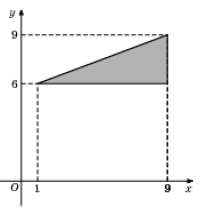
| |
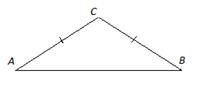
4. В треугольнике ABC AC = BC, угол С равен 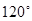 , ,  , найдите , найдите  . .
|
| |
5. Найдите высоту равностороннего треугольника со стороной 
| 
| |
| 6. В прямоугольном треугольнике один из углов равен 400 Найдите внешний угол при вершине второго острого угла. Ответ дайте в градусах. 6. | ||
7. Найдите ( в  ) площадь закрашенной
фигуры, изображенной на клетчатой бумаге с
размером клетки ) площадь закрашенной
фигуры, изображенной на клетчатой бумаге с
размером клетки 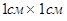 (см. рис.) В ответе запишите (см. рис.) В ответе запишите 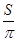
| 
| |
| 8. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300 . Найдите боковую сторону треугольника, если его площадь равна 1089. | |
| 9. Найдите тангенс угла АОВ, изображенного на рисунке | 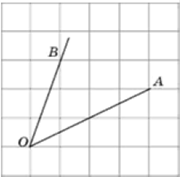
|
| 10. Какие из следующих утверждений верны? 1). Центром окружности, описанного около правильного треугольника, является точка пересечения высот. 2). В любой четырехугольник можно вписать не более одной окружности. 3). Если стороны прямоугольника равны 3 и 4, то диаметр описанной около него окружности равен 5. | |
| 11. Площадь треугольника АВС равна 16. Найти длину стороны АВ, если АС = 5, ВС = 8 и угол С – тупой. | |
12. Найдите площадь прямоугольного треугольника с острым углом 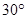 и гипотенузой, равной 4. и гипотенузой, равной 4.
| |
| 13. Площадь равнобедренного прямоугольного треугольника равна 36. Найдите длину гипотенузы. | |
| 14. Найдите градусную меру острого угла между биссектрисами острых углов прямоугольного треугольника. | |
| 15. Катеты прямоугольного треугольника равны 30 и 40. Найдите медиану, проведенную к гипотенузе. | |
| 16. Высота прямоугольного треугольника, проведенная к гипотенузе, делит ее на отрезки, длины которых относятся как 1:4. Если высота равна 4, то гипотенуза равна… | |
| 17*. В треугольнике АВС из вершины В проведена медиана и высота, которые делят угол АВС на три равные части. Найти углы треугольника АВС. | |
| 18*. Длины сторон треугольника относятся как 5:12:13. Соединив середины его сторон, получили треугольник площадью 30. Найдите периметр исходного треугольника. | |
| 19*. Три высоты треугольника АВС пересекаются в точке О внутри треугольника, причём ОС = АВ. Найдите угол АСВ. |