Вероятность события при многократных испытаниях

Если производится несколько испытаний и в каждом из них вероятность события А не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А (выборка с возвратом).

Сложное событие – определенная комбинация нескольких простых событий (исходов испытаний).

Если вероятность события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность сложного события, состоящего в том, что в «n» однородных испытаниях событие А наступит «K» раз, равна (формула Бернулли):

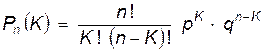, (1.11)

где p – вероятность события А в одном испытании;

q =(1 – p) – вероятность непоявления события А в испытании.

Пример.

Вероятность проектного натяжения высокопрочных болтов равна p=0.95. Найти вероятность того, что из пяти проверенных болтов два окажутся недотянуты.

Подставляем в формулу (11) значения n=5; K=2; p=0,95; q=0,05:

.

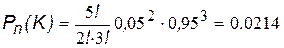При достаточно больших значениях n и K пользоваться формулой Бернулли крайне неудобно. В этих случаях вероятность Р_n(К) можно оценить приближенно по формуле Лапласа:

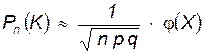(1.12)

где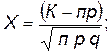

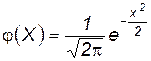(табличная функция). (1.13)

Чем больше n , тем точнее формула (1.12).

Пример.

Вероятность проектного натяжения высокопрочных болтов равна 0.97. Найти вероятность того, что из 20 проверенных болтов 2 окажутся недотянуты.

Применим в данном случае формулу (1.12) Лапласа. При этом n=20; K=2; p=0,03; q=0,97. Вычисляем 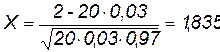. Далее по таблице находим 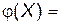0,074. И, наконец, по формуле (1.12) находим .

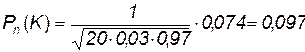Интегральная формула:

Вероятность Р_n (К₁, К₂) того, что событие А в n испытаниях появится от К₁ до К₂ раз, приближенно равна:

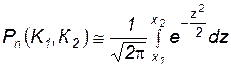, ( 1.13 )

где , .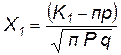

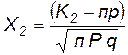Интеграл 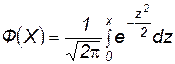- табличный (функция Лапласа).

Контрольные вопросы

1. Дайте определение понятия вероятность.

2. Дайте определение суммы и произведения двух событий.

3. Что такое условная вероятность?

4. Как определить вероятность сложного события?