Вероятность произведения событий. Независимость событий.

Теорема 3.Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого, при условии, что первое событие произошло:

. (1)

По определению, событие В не зависит от события А, если

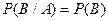. (2)

В этом случае также 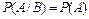, т.е. событие А не зависит от события В. Свойство независимости событий является взаимным. Если события А и В независимы, то независимы события и , и , и . Если события А и В независимы, то формулы (1) с учетом равенства (2) принимают вид

,

т.е. вероятность произведения независимых событий равна произведению их вероятностей.

Пример.

В урне 10 шаров, из которых 4 белые. Наугад выбираются 3 шара. Найти вероятность того, что хотя бы один шар белый.

Решение.

Пусть событие А – хотя бы один шар из трех вынутых – белый, наступит, если будет осуществлено любое из трех несовместных событий: B - один шар белый, C - два шара белые, D - три шара белые. Имеем . По теореме 1: 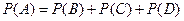. Вероятности событий B, C, D численно равны

.

Отсюда

.

 

Пример.

Вероятность попадания в цель при одном залпе двух стрелков равна 0,38. Найти вероятность поражения цели при одном выстреле первым стрелком, если известно, что вероятность поражения цели вторым стрелком равна 0,8.

Решение.

Пусть событие А₁ – попадет в цель первый стрелок, А₂ – второй, тогда соответствующие вероятности . Пусть событие D – цель поражена, тогда

.

Следовательно,

.

Так как по условию

,

то получаем

.