Главные нормальные напряжения

Инварианты тензора напряжения

Площадки, на которых отсутствуют касательные напряжения, называются площадками главных нормальных напряжений s₁₁ , s₂₂ , s₃₃ . Индексы при последних назначаются по правилу

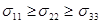
т.е. индекс "1" присваивается большему, а "3" – меньшему из значений.

Тензор напряжений, записанный в ортогональной системе координат, совпадающей с направлениями главных напряжений, имеет вид

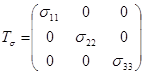(1.3)

Это означает, что напряженное состояние в любой точке деформируемого тела вызвано чистым растяжением или сжатием по трем взаимно перпендикулярным главным направлениям.

Главные напряжения являются корнями кубического уравнения

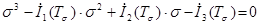(1.4)

Коэффициенты 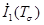, , 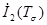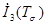этого уравнения называются инвариантами тензора напряжений. В произвольной ортогональной системе координат и ортогональной системе координат, совпадающей с направлениями главных нормальных напряжений они имеют вид

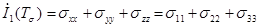
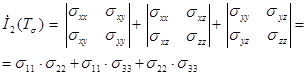(1.5)

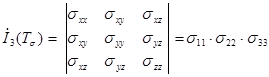
Величина, составленная из первого инварианта

(1.6)

называется средним ( или гидростатическим ) давлением в точке и имеет большое значение в теории пластичности и теории ОМД. В тензорной форме она записывается так :

 

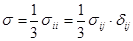
Девиатор тензора напряжения и его инварианты

Так как материалы обладают, как правило, различными механическими свойствами по отношению к сдвигу и равномерному всестороннему сжатию, целесообразно представить тензор напряжения в виде суммы двух тензоров

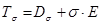(1.7)

Здесь s × Е – так называемый шаровой тензор, соответствующий среднему давлению в некоторой точке деформируемого тела и отвечающий за изменение его объема.

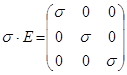, ( Е - единичный тензор )

а 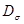– тензор, характеризующий касательные напряжения в той же точке, называется девиатором напряжения и отвечает за изменение формы. Он характеризует насколько заданное напряженное состояние отличается от всестороннего равного растяжения или сжатия с главными напряжениями равными s .

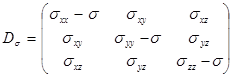
Главные направления девиатора напряжения 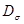и тензора напряжения Т_s совпадают, а главные значения S₁₁ , S₂₂ , S₃₃ отличаются от s₁₁ , б₂₂, s₃₃ на величину среднего давления s .

Компоненты девиатора 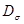будем обозначать через S_ij . Тогда компоненты тензора Т_s можно представить через компоненты девиатора 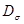и шарового тензора s × Е так :

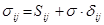(1.8)

Инварианты девиатора напряжения имеют вид:

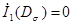
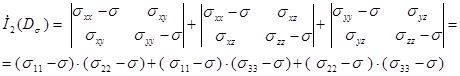(1.9)

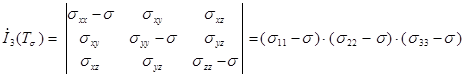
Большую роль в теории пластичности играет второй инвариант. Неотрицательную величину

(1.10)

называют интенсивностью касательных напряжений. В главных напряжениях она имеет вид

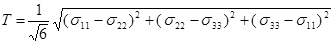(1.11)

В тензорной форме она запишется так

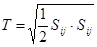(1.12)

Интенсивность касательных напряжений обращается в нуль, когда напряженное состояние является состоянием гидростатического давления

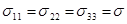
Для чистого сдвига

; ;

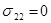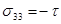
Здесь t – напряжение чистого сдвига. Следовательно

В случае одноосного растяжения ( сжатия ) в направлении, например, оси Х

 

; ;

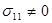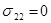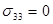
Тогда

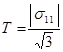(1.13)