Основные определения. Тензор напряжения.

ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ

В однородном поле напряжение – это сила, которая приходится на единицу площади некоторого сечения, мысленно выделенного в теле. Причем эта сила показывает как действует отброшенная часть тела на оставшуюся.

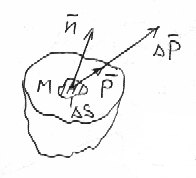На рисунке показана оставшаяся часть тела и вектор силы , которая действует от отброшенной части тела на элемент поверхности сечения , внешняя единичная нормаль к которому . Тогда более точно напряжение, действующее в точке М сечения запишется так

 

 

Рассмотрим в некоторой точке деформируемого тела бесконечно малый тетраэдр. По каждой грани выделенного из тела тетраэдра действуют свои векторы напряжений .

 

Подстрочные индексы показывают, как направлена нормаль к площадке, на которой они действуют ( напряжение 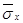действует по площадке, нормаль к которой параллельна оси Х и т.д. ) . Напряжение на наклонной площадке .

 

Каждый из указанных векторов напряжений 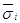можно задать его проекциями на координатные оси

 

Здесь второй индекс у указывает координатную ось на которую проецируется напряжение 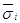. Величины s_xy , s_xz , s_yx , s_yz , s_zx , s_zy - компоненты векторов напряжений, лежащие в плоскостях граней тетраэдра соответственно ВОС, АОС, АОВ – называются касательными напряжениями. Величины s_xx , s_yy , s_zz – являются компонентами напряжений 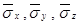, перпендикулярными к граням тетраэдра и называются нормальными напряжениями.

Если заданы компоненты напряжений по трем взаимно перпендикулярным площадкам, проходящим через данную точку деформируемого тела, то напряжения на любой площадке, наклонной к координатным плоскостям можно подсчитать по формулам.

(1.1)

Здесь n_x , n_y , n_z – направляющие косинусы наклонной площадки по отношению к координатным плоскостям.

Коэффициенты (напряжения) при направляющих косинусах n_i в уравнениях (1.1.) образуют так называемый тензор напряжения

(1.2)

содержащий шесть существенных компонент, т.к. является симметричным ( s_ij = s_ji , т.е. s_xy = s_yx и т.д. ) .