Экспоненциальный рост численности.
Лабораторная работа №1.
«Динамика численности популяций».
Моделирование динамики популяции с помощью расчетной программы
Цель работы: Изучить модели динамики численности популяции с помощью расчетной программы.
К работе допущен
Работу выполнил
Работу защитил
2010г.
1 ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Согласно определению известного русского эколога С.С.Шварца, популяция – это элементарная группировка организмов определенного вида, обладающая всеми необходимыми условиями для поддержания своей численности длительное время в постоянно изменяющихся условиях среды.
Популяции, как и любой биологической открытой системе, свойственны определенная структура, рост, развитие, устойчивость к абиотическим и биотическим факторам.
Наиболее важным показателем благополучия популяции (устойчивости), ее роли в функционировании природной экосистемы является ее численность.
Численность популяции определяется в основном двумя явлениями – рождаемостью и смертностью, а также миграцией.
Рождаемость - количество новых особей, появившихся в единицу времени в результате размножения. В процессе размножения число особей возрастает, теоретически она способна к неограниченному росту численности.
Существуют различные типы изменения численности особей в популяции в зависимости от времени (динамики популяции). В наиболее простых случаях динамика популяции может быть описана несложными математическими моделями, которые позволяют прогнозировать изменение численности особей.
Экспоненциальный рост численности.
Одна из наиболее ранних моделей роста численности особей популяции была предложена Т. Мальтусом 1798 году, в широко известной работе "О принципах народонаселения". Данная модель получила название экспоненциальной зависимостироста численности (экспоненциальной кривой роста). В данной моделипредполагаетсянеограниченное количество природных ресурсов,доступных особям популяции, и отсутствие каких-либо сдерживающих факторовдля роста численности. При таких допущениях численность особей в популяции возрастает по степенной зависимости, т.е. очень быстро и неограниченно.
Если обозначить через n0 количество особей в популяции и начальный момент времени (t0), а через Nt количество особей в некоторый момент времени t (t>t0). Тогда изменение численности ∆N за интервал времени ∆t. т.е. скорость роста популяции будет равна:

 (1)
(1)
В выражении (1) приведена средняя скорость роста популяции. Однако в популяционной экологии чаще используется не абсолютная средняя скорость, а скорость роста на один организм (специфическая скорость):
 (2)
(2)
Данный показатель позволяет сравнивать значения изменение численности популяциях разных размеров. В этом случае численность определяется как скорость увеличения на одну особь за определенный интервал времени.
Перейдя к предельной форме записи скорости при  0 и
0 и  и введя новое обозначение:
и введя новое обозначение:
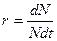 (3)
(3)
В выражении (3)показатель r может быть определен как мгновенная удельная скорость роста популяции. Для различных популяций одного того же вида это показатель может иметь различные значения. Наибольшее из всех возможны значений (rmax) называют биотическим или репродуктивным потенциалом популяции
С учетом выражения (3) скорость роста популяции можно описать следующим выражением
 (4)
(4)
Продифференцировав выражение (4) получим, что в любой момент времени при условии r=сonst (константа скорости роста) численность особей в популяции будет равна:  (5)
(5)
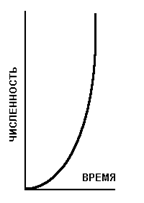
Формула (5) описывает экспоненциальную модель роста популяции, которая в графическом виде имеет форму кривой (рис.1). Экспоненциальная модель роста отвечает условиям неограниченного роста численности особей в популяции.
Рис. 1.Экспоненциальная кривая роста численности особей в популяции