Гипергеометрическая вероятность.

Пример 4. Задача. Из урны, в которой белых и черных шаров, наудачу, без возвращения вынимают 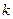шаров, . Термин «наудачу» означает, что появление любого набора из 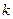шаров равновозможно. Найти вероятность того, что будет выбрано ровно белых и черных шаров.

По смыслу задачи понятно, что и .

Результатом эксперимента является набор из 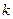шаров. При этом можно не учитывать или учитывать порядок следования шаров.

1. Выбор без учета порядка. Общее число элементарных исходов есть число способов выбора 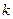- шаров из элементов.

Обозначим через событие, вероятность которого требуется найти. Событию благоприятствует появление любого набора, содержащего белых шаров и черных. Число благоприятных исходов равно произведению (по теореме о перемножении шансов) числа способов выбрать белых шаров из и числа способов выбрать черных шаров из . Таким образом, вероятность события равна

(1)

2. Выбор с учетом порядка. Общее число элементарных исходов есть число способов разместить элементов на 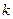местах:

.

При подсчете числа благоприятных исходов нужно учесть как число способов выбрать нужное число шаров, так и число способов расположить эти шары среди 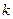мест. Можно, скажем, посчитать число способов выбрать мест среди 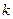(равное ), затем число способов разместить на этих местах белых шаров (равное — не забывайте про учет порядка!), и затем число способов разместить на оставшихся местах черных шаров (равное ). Перемножив эти числа, получим формулу для вычисления искомой вероятности

.

Таким образом, в обоих случаях мы получаем одинаковый результат.