Свойства эмпирической дисперсии

1. Дисперсия постоянной величины равна нулю.

2. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то дисперсия не изменится.

3. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число k раз, то дисперсия уменьшится (увеличится) в k² раз.

4. Эмпирическая дисперсия равна разности между средней арифметической квадратов наблюдений и квадратом средней арифметической .

Пример 38. Найти эмпирическую дисперсию и выборочное среднее квадратическое отклонение для следующего интервального вариационного ряда

Интервалы	3 – 7	7 - 11	11 - 15	15 - 19	19 - 23	23 – 27
Частоты

Решение. Эмпирическую дисперсию найдём по формуле и где - середины интервалов

- соответствующая частота, тогда

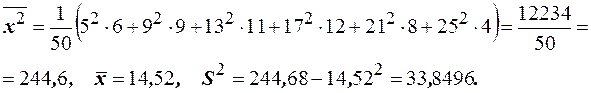
35. Эмпирические центральные и начальные моменты

Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда.

О.1. Эмпирическим начальным моментом порядка k называют взвешенную среднюю арифметическую k-х степеней вариантов .

О.2. Эмпирическим центральным моментом порядка k называют взвешенную среднюю арифметическую k-х степеней отклонений вариантов от их средней арифметической .

Эмпирический центральный момент нулевого порядка равен .

Эмпирический центральный момент первого порядка равен .

Эмпирический центральный момент второго порядка равен .

Эмпирический центральный момент третьего порядка равен .

Эмпирический центральный момент четвёртого порядка равен .

Рассмотрим свойства центральных моментов, которые позволяют значительно упростить их вычисление.

1. Если все варианты уменьшить (увеличить) на одно и то же число, то центральный момент k-го порядка не изменится.

2. Если все варианты уменьшить (увеличить) в одно и то же число q раз, то центральный момент k-го порядка уменьшится (увеличится) в раз.

36. Эмпирические асимметрия и эксцесс

Эмпирическим коэффициентом асимметрии называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения .

Если полигон вариационного ряда скошен, то есть одна из его ветвей, начиная от вершины, зримо длиннее другой, то такой ряд называют асимметричным. Если в вариационном ряду преобладают варианты, меньшие , то эмпирический коэффициент асимметрии отрицателен, и в этом случае имеет место левосторонняя асимметрия. Если же в вариационном ряду преобладают варианты, большие , то эмпирический коэффициент асимметрии положителен, и в этом случае имеет место правосторонняя асимметрия. При левосторонней асимметрии левая ветвь длиннее правой. При правосторонней, более длинной является правая ветвь.

Эмпирический коэффициент асимметрии не имеет ни верхней, ни нижней границы, что снижает его ценность как меры асимметрии. Практически коэффициент асимметрии редко бывает особенно велик, а для умеренно асимметричных рядов он обычно меньше единицы.

Эмпирическим эксцессом или коэффициентом крутости называют уменьшенное на три единицы отношение центрального момента четвёртого порядка к четвёртой степени среднего квадратического отклонения: .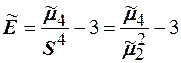

За стандартное значение эксцесса принимают нуль-эксцесс нормальной кривой распределения. Кривые, у которых эксцесс отрицательный, по сравнению с нормальной менее крутые, имеют более плоскую вершину и называются «плосковершинными». Кривые с положительным эксцессом более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются «островершинными».

Т. Коэффициенты асимметрии и эксцесса не зависят от выбора начало отсчёта и единицы измерения, то есть для любых постоянных и b, , .

Доказательство. По свойствам эмпирических центральных моментов имеем 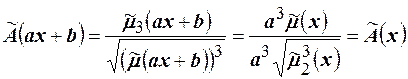и .

37. Метод условных вариантов для расчёта основных

числовых характеристик вариационного ряда

Значения вариантов могут быть достаточно большими, и, следовательно, вычисление числовых характеристик достаточно трудоёмко. Поэтому для дискретного вариационного ряда при вычислении коэффициентов асимметрии и эксцесса желательно перейти к условным вариантам по формуле , где h- шаг вариационного ряда, С- ложный ноль, то есть вариант, имеющий либо наибольшую частоту, либо равноудаленный от максимального и минимальных вариантов. Тогда основные числовые характеристики для вариантов x и u связаны соотношениям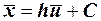и ; и .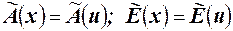

Пример 39. Перейдя к условным вариантам, вычислить эмпирические коэффициенты асимметрии и эксцесса для интервального вариационного ряда.

Интервалы	[3 – 7)	[7 – 11)	[11 – 15)	[15 – 19)	[19 – 23)	[23 – 27)
Частоты

Решение. Шаг интервального вариационного ряда равен h=4. Интервал, имеющий наибольшую частоту , то за условный ноль примем его середину С=17. Перейдём к условным вариантам по формуле . Тогда получим дискретный вариационный ряд.

u_i	-3	-2	-1
m_i

Найдём эмпирические начальные моменты:

;

Найдём эмпирические центральные моменты:

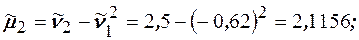
Тогда среднее арифметическое равно

Эмпирическая дисперсия равна

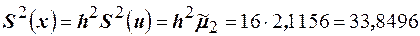Эмпирический коэффициент асимметрии равен

параметра называют состоятельной, если она подчиняется закону больших чисел, то есть при достаточно большом числе независимых наблюдений п с вероятностью, близкой к единице, можно утверждать, что разность между и по абсолютной величине окажется меньше сколь угодно малого числа , или , где - положительное число, близкое к нулю.

На практике при оценке параметров не всегда удаётся удовлетворить одновременно требованиям несмещённости, эффективности и состоятельности оценки. Так, например, может оказаться, что для простоты расчётов целесообразно использовать незначительно смещённую оценку. Однако выбору оценки всегда должно предшествовать её критическое рассмотрение со всех точек зрения.

40. Оценка математического ожидания и дисперсии

Наиболее важными числовыми характеристиками случайной величины являются математическое ожидание и дисперсия. Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают математическое ожидание и дисперсию.

Т.1. Средняя арифметическая , вычисленная по п независимым наблюдениям над случайной величиной Х, которая имеет математическое ожидание , является несмещённой оценкой этого параметра.

Доказательство. Пусть независимые наблюдения над случайной величиной. По определению . Найдём . Следовательно: .

Т.2. Средняя арифметическая , вычисленная по п независимым наблюдениям над случайной величиной, которая имеет математическое ожидание и дисперсию , является состоятельной оценкой этого параметра.