Повторные независимые испытания

В главе рассматриваются:

- формула Бернулли;

- формула Пуассона;

- локальная и интегральная формулы Муавра-Лапласа.

Типовые задачи

Пример 2.1

В среднем 20% пакетов акций на аукционах продаются по первоначально заявленной цене. Найти вероятность того, что из 9 пакетов акций в результате торгов по первоначально заявленной цене:

1) не будут проданы 5 пакетов;

2) будет продано:

а) менее 2 пакетов;

б) не более 2;

в) хотя бы 2 пакета;

г) наивероятнейшее число пакетов.

Решение

1) Вероятность того, что пакет акций не будет продан по первоначально заявленной цене, р = 1-0,2 = 0,8.

По формуле Бернулли (2.1)

2.а) По условию p = 0,2

2.б)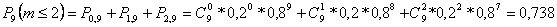

2.в)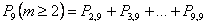

Указанную вероятность можно найти проще, если перейти к противоположному событию, т.е.

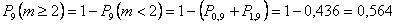(см.п.2а).

2.г) Наивероятнейшее число проданных акций по первоначально заявленной цене определится из условий (2.4), т.е.

9*0,2-0,8 ≤ m₀ ≤ 9*0,2+0,2 или 1≤ m₀ ≤ 2,

т.е. наивероятнейших чисел два: m₀ = 1 и 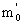= 2.

Поэтому вероятность

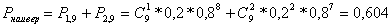
Пример 2.2

Завод отправил на базу 10000 стандартных изделий. Среднее число изделий, повреждаемых при транспортировке, составляет 0,02%. Найти вероятность того, что из 10000 изделий:

1) будет повреждено:

а) 3;

б) по крайней мере 3;

2) не будет повреждено:

а) 9997;

б) хотя бы 9997.

Решение

1.а) Вероятность того, что изделие будет повреждено при транспортировке, равна р = 0,0002. Так как р – мала, n = 10000 – велико и λ = n*p = 10000*0,0002 = 2≤10, следует применить формулу Пуассона (2.6):

.

Это значение проще найти, используя табл. III приложений:

P_3,10000 = P₃(2) = 0,1804

1.б) Вероятность P₁₀₀₀₀(m ≥ 3) может быть вычислена как сумма большого количества слагаемых:

P₁₀₀₀₀(m ≥ 3) = P_3,10000+ P_4,10000+…+ P_10000,10000.

Но, разумеется, проще ее найти, перейдя к противоположному событию:

P₁₀₀₀₀(m ≥ 3) = 1 - P₁₀₀₀₀(m < 3) = 1 - (P_0,10000+P_1,10000+ P_2,10000) = 1-(0,1353+0,2707+0,2707) = 0,3233.

Следует отметить, что для вычисления вероятности P₁₀₀₀₀(m ≥ 3) = P₁₀₀₀₀(3 ≤ m ≤ 10000) нельзя применить интегральную формулу Муавра-Лапласа, так как не выполнено условие ее применимости, ибо npq ≈ 2 < 20.

2.а) В данном случае p = 1-0,0002 = 0,9998 и надо найти P_9997,10000, для непосредственного вычисления которой нельзя применить ни формулу Пуассона (р велика), ни локальную формулу Муавра-Лапласа (npq ≈ 2 < 20). Однако событие «не будет повреждено 9997 из 10000», вероятность которого, равна 0,1804, получена в 1.а).

2.б) Событие «не будет повреждено хотя бы 9997 из 10000» равносильно событию «будет повреждено не более 3 из 10000», для которого p = 0,0002 и

P₁₀₀₀₀(m ≤ 3) = P_0,10000+ P_1,10000+ P_2,10000+ P_3,10000 = 0,1353+0,2707+0,2707+0,1805 = 0,8572.

Пример 2.3

По результатам проверок налоговыми инспекциями установлено, что в среднем каждое второе малое предприятие региона имеет нарушение финансовой дисциплины. Найти вероятность того, что из 1000 зарегистрированных в регионе малых предприятий имеют нарушения финансовой дисциплины:

а) 480 предприятий;

б) наивероятнейшее число предприятий;

в) не менее 480;

г) от 480 до 520

Решение

а) По условию р = 0,5. Так n = 1000 достаточно велико (условие npq = 10000*0,5*(1-0,5) = 250 ≥ 20 выполнено), то применяем локальную формулу Муавра-Лапласа. Вначале по (2.9) определим

,

затем по формуле (2.7)

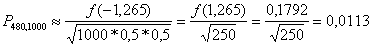
б) По формуле (2.6) наивероятнейшее число 1000*0,5-0,5 ≤ m₀ ≤ 1000*0,5+0,5, т.е. 499,5≤m₀≤500,5 и целое m₀ = 500.

Теперь по (2.9) определим

и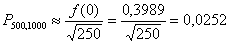

в) Необходимо найти

P₁₀₀₀(

m≥480) =

P₁₀₀₀(480 ≤

m ≤ 1000). Применяем интегральную формулу Муавра-Лапласа (2.10), предварительно найдя по формуле (2.12)

,

Теперь

P₁₀₀₀(480≤m≤1000) ≈ 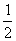[Ф(31,6) – Ф(-1,265)] = 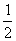[Ф(31,6) + Ф(1,265)] ≈ 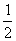*(1+0,7941) ≈ 0,897.

г) Вероятность Р₁₀₀₀(480 ≤ m ≤520) можно было найти по той же интегральной формуле Муавра–Лапласа (2.10). Но проще это сделать, используя следствие (2.13), заметив, что границы интервала 480 и 520 симметричны относительно значения пр = 1000*0,5 = 500:

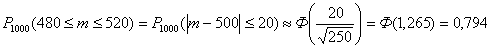
Пример 2.4

В страховой компании 10 тыс. клиентов. Страховой взнос каждого клиента составляет 500 руб. При наступлении страхового случая, вероятность которого по имеющимся данным и оценкам экспертов можно считать равной р = 0,005, страховая компания обязана выплатить клиенту страховую сумму размером 50 тыс. руб. На какую прибыль может рассчитывать страховая компания с надежностью 0,95?

Решение

Размер прибыли компании составляет разность между суммарным взносом всех клиентов и суммарной страховой суммой, выплаченной n₀клиентам при наступлении страхового случая, т.е.

П = 500*10-50n₀ = 50(100-n₀) тыс.руб.

Для определения n₀применим интегральную формулу Муавра-Лапласа (требование npq = 10000*0,005*0,995 = 49,75 > 20 выполнено).

По условию задачи

, (2.17)

где т – число клиентов, которым будет выплачена страховая сумма;

,

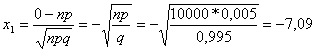откуда

Из соотношения (2.17)

Ф(х₂) = 1,9 + Ф(х₁) = 1,9 + Ф(-7,09) ≈ 1,9+(-1) = 0,9

По табл. II приложений Ф(х₂) = 0,9 при х₂ = 1,645

Теперь и ,

т.е. с надежностью 0,95 ожидаемая прибыль составит 1,92 млн.руб.

Задания

2.1. Вероятность малому предприятию быть банкротом за время t равна 0,2. Найти вероятность того, что из шести малых предприятий за время t сохранятся:

а) два;

б) более двух.

2.2. В среднем пятая часть поступающих в продажу автомобилей некомплектны. Найти вероятность того, что среди десяти автомобилей имеют некомплектность:

а) три автомобиля;

б) менее трех.

2.3. Производится залп из шести орудий по некоторому объекту. Вероятность попадания в объект из каждого орудия равна 0,6. Найти вероятность ликвидации объекта, если для этого необходимо не менее четырех попаданий.

2.4. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы:

а) три договора;

б) менее двух договоров.

2.5. Предполагается, что 10% открывающихся новых малых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из шести малых предприятий не более двух в течение года прекратят свою деятельность?

2.6. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:

а) не менее трех мальчиков;

б) не более трех мальчиков.

2.7. Два равносильных противника играют в шахматы. Что более вероятно:

а) выиграть 2 партии из 4 или 3 партии из 6;

б) не менее 2 партий из 6 или не менее 3 партий из 6?

(Ничьи в расчет не принимаются.)

2.8. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено:

а) три ошибочно укомплектованных пакета;

б) не более трех пакетов.

2.9. Строительная фирма, занимающаяся установкой летних коттеджей, раскладывает рекламные листки по почтовым ящикам. Прежний опыт работы компании показывает, что примерно в одном случае из двух тысяч следует заказ. Найти вероятность того, что при размещении 100 тыс. листков число заказов будет:

а) равно 48;

б) находиться в границах от 45 до 55.

2.10. В вузе обучаются 3650 студентов. Вероятность того, что день рождения студента приходится на определенный день года, равна 1/365. Найти: а) наиболее вероятное число студентов, родившихся 1 мая, и вероятность такого события; б) вероятность того, что по крайней мере 3 студента имеют один и тот же день рождения.

2.11. Учебник издан тиражом 10 000 экземпляров. Вероятность того, что экземпляр учебника сброшюрован не правильно, равна 0,0001. Найти вероятность того, что:

а) тираж содержит 5 бракованных книг;

б) по крайней мере 9998 книг сброшюрованы правильно.

2.12. Баскетболиста делают по 3 броска мячом в корзину. Вероятности попадания мяча в корзину при каждом броске равны соответственно 0,6 и 0,7. Найти вероятность того, что:

а) у обоих будет одинаковое количество попаданий;

б) у первого баскетболиста будет больше попаданий, чем у второго.

2.13. Известно, что в среднем 60% всего числа изготовляемых заводом телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в изготовленной партии окажется:

а) 6 аппаратов первого сорта, если партия содержит 10 аппаратов;

б) 120 аппаратов первого сорта, если партия содержит 200 аппаратов?

2.14. Вероятность того, что перфокарта набита оператором неверно, равна 0,1. Найти вероятность того, что:

а) из 200 перфокарт правильно набитых будет не меньше 180;

б) у того же оператора из десяти перфокарт будет неверно набитых не более двух.

2.15. Аудиторную работу по теории вероятностей с первого раза успешно выполняют 50% студентов. Найти вероятность того, что из 400 студентов работу успешно выполнят:

а) 180 студентов;

б) не менее 180 студентов.

2.16. При обследовании уставных фондов банков установлено, что пятая часть банков имеют уставный фонд свыше 100 млн. руб. Найти вероятность того, что среди 1800 банков имеют уставный фонд свыше 100 млн. руб.:

а) не менее 300;

б) от 300 до 400 включительно.

2.17. Сколько нужно взять деталей, чтобы наивероятнейшее число годных деталей было равно 50, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,1?

2.18. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,01. Найти наиболее вероятное число опоздавших из 800 пассажиров и вероятность такого числа опоздавших.

2.19. Вероятность того, что деталь стандартна, равна р = 0,9. Найти:

а) с вероятностью 0,9545 границы (симметричные относительно р), в которых заключена доля стандартных среди проверенных 900 деталей;

б) вероятность того, что доля нестандартных деталей среди них заключена в пределах от 0,08 до 0,11.

2.20. В результате проверки качества приготовленных для посева семян гороха установлено, что в среднем 90% всхожи. Сколько нужно посеять семян, чтобы с вероятностью 0,991 можно было ожидать, что доля взошедших семян отклонится от вероятности взойти каждому семени не более, чем на 0,03 (по абсолютной величине)?

2.21. Вероятность того, что дилер, торгующий ценными бумагами, продаст их, равна 0,7. Сколько должно быть ценных бумаг, чтобы можно было утверждать с вероятностью 0,996, что доля проданных среди них отклонится от 0,7 не более, чем на 0,04 (по абсолютной величине)?

2.22. У страховой компании имеются 10 000 клиентов. Каждый из них, страхуясь от несчастного случая, вносит 500 руб. Вероятность несчастного случая 0,0055, а страховая сумма, выплачиваемая пострадавшему, составляет 50 000 руб. Какова вероятность того, что:

а) страховая компания потерпит убыток;

б) на выплат страховых сумм уйдет более половины всех средств поступивших от клиентов?

2.23. Первый прибор состоит из 10 узлов, второй из 8 узлов. За время tкаждый из узлов первого прибора выхода из строя, независимо от других, с вероятностью 0,1, второго – с вероятностью 0,2. Найти вероятность того, что за время t в первом приборе выйдет из строя хотябы один узел, а во втором – по крайней мере два узла.

2.24. Студент рассматриваемого вуза по уровню подготовленности с вероятностью 0,3 является «слабым», с вероятностью 0,5 – «средним», с вероятностью 0,2 – «сильным». Какова вероятность того, что из наудачу выбранных 6 студентов вуза:

а) число «слабых», «средних» и «сильных» окажется одинаковым;

б) число «слабых» и «сильных» окажется одинаковым?

ГЛАВА