Алгебра событий
Определение 2.1. Испытание (опыт) – это осуществление некоторого комплекса условий, в которых наблюдается случайный процесс или явление.
Определение 2.2. Полем событий (пространством элементарных исходов) 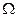 называют совокупность всех исходов испытаний (опыта). Элементы
называют совокупность всех исходов испытаний (опыта). Элементы 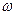 этого множества называются элементарными событиями (элементарными исходами),
этого множества называются элементарными событиями (элементарными исходами), 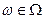 .
.
Определение 2.3. Случайным событием или просто событием будем называть подмножество 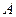 множества
множества 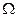 ,
,  .
.
Определение 2.4. Операции над событиями:
-говорят, что событие 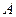 благоприятствует событию
благоприятствует событию 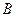 , если как только произошло событие
, если как только произошло событие 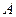 , то произошло событие
, то произошло событие 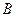 (рис. 1). Обозначают
(рис. 1). Обозначают 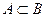 .
.
-говорят, что событие 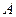 равносильно событию
равносильно событию 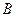 , если событие
, если событие 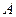 благоприятствует событию
благоприятствует событию 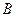 , а
, а 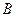 благоприятствует
благоприятствует 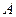 . Обозначают
. Обозначают 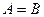 .
.
- событие  называется объединением событий
называется объединением событий 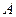 и
и 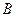 , если событие
, если событие  происходит тогда и только тогда, когда происходит либо
происходит тогда и только тогда, когда происходит либо 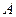 , либо
, либо 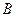 , либо
, либо 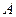 и
и 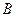 вместе (рис. 2). Обозначают
вместе (рис. 2). Обозначают  .
.
- событие  называется пересечением событий
называется пересечением событий 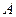 и
и 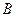 , если событие
, если событие  происходит тогда и только тогда, когда происходят события
происходит тогда и только тогда, когда происходят события 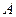 и
и 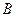 вместе (рис. 3). Обозначают
вместе (рис. 3). Обозначают 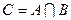 .
.
- событие  называется разностью событий
называется разностью событий 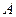 и
и 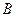 , если событие
, если событие  происходит тогда и только тогда, когда событие
происходит тогда и только тогда, когда событие 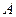 происходит, а
происходит, а 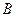 не происходит (рис. 4). Обозначают
не происходит (рис. 4). Обозначают  .
.
Пространство элементарных исходов 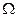 - достоверное событие, пустое множество
- достоверное событие, пустое множество 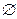 - невозможное событие.
- невозможное событие.

| |||
| рис. 1 | рис. 2 | рис. 3 | рис. 4 |
Определение 2.5.События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании, то есть  .
.
Определение 2.6. Говорят, что события 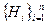 образуют полную группу, если любые два из них несовместны и хотя бы одно непременно должно произойти в результате испытания:
образуют полную группу, если любые два из них несовместны и хотя бы одно непременно должно произойти в результате испытания: 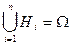 ,
,  для любых
для любых 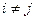 .
.
Определение 2.7. Событие 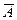 называется противоположным событию
называется противоположным событию 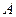 , если
, если 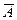 происходит тогда и только тогда, когда
происходит тогда и только тогда, когда 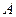 не происходит,
не происходит, 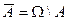 .
.
Можно дать еще одно определение противоположного события.
Определение 2.8. Событие 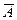 называется противоположным событию
называется противоположным событию 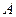 , если выполнены следующие условия: 1)
, если выполнены следующие условия: 1)  ; 2)
; 2)  .
.