Вторая задача динамики заключается в определении закона движения по заданным силам и начальным условиям.

Определение: начальными условиями называются значения координат и проекций скоростей в тот момент времени, который принимают за начало отсчета:

Начальные условия для материальной точки:

Вторая задача является обратной по отношению к первой задачи динамики, поэтому решается двукратным интегрированием дифференциальных уравнений движения. Сложность заключается в том, что не каждую задачу можно свести к квадратурам, не говоря уже о вычислении соответствующих интегралов. В этом случае часто прибегают к методу численного интегрирования с помощью ЭВМ.

При каждом интегрировании добавляются постоянные интегрирования, которые определяются из начальных условий, поэтому полученный закон движения выражается через начальные условия:

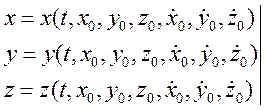(20)

1.5 Основные виды прямолинейного движения точки

При прямолинейном движении скорость и ускорение точки все время направлены вдоль траектории точки. Вводим координатные оси. В динамике одну из осей координат направляют вдоль траектории движения точки, а вторую перпендикулярно движению, таким образом, чтобы поворот от одной оси к другой был виден против часовой стрелки. Дифференциальное уравнение прямолинейного движения точки имеет вид:

(21)

Начальные условия задачи задаются в виде:

При .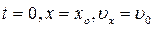

Наиболее простыми примерами прямолинейного движения материальной точки являются примеры, когда сила зависит от одного параметра, (например, постоянная сила; сила, зависящая от координаты (сила упругости); сила, зависящая от времени или скорости).

1.6 Криволинейное движение материальной точки

Одним из наиболее важных приложений законов движения свободной материальной точки является задача о движении точки под действием силы тяжести в плоскости с учетом и без учета сопротивления среды.

Примеры прямолинейного и криволинейного движения материальной точки (пункты 1.5 и 1.6) рассматриваются на практических занятиях.

1.7 Относительное движение материальной точки

Основное уравнение динамики справедливо только в инерциальной системе отсчета.

Рассмотрим движение точки массой m в двух системах отсчета: инерциальной O₁x₁y₁z₁ и неинерциальной Oxyz, считая первую из них неподвижной, а вторую подвижной системой отсчета. Движение точки по отношению к инерциальной системе отсчета абсолютное, по отношению к неинерциальной системе отсчета относительное, а движение неинерциальной системы отсчета по отношению к инерциальной системе отсчета переносное. В соответствие с теоремой Кориолиса абсолютное ускорение складывается из векторной суммы относительного, переносного и кориолисова ускорений

. (22)

Основное уравнение динамики будет справедливым, если под абсолютным ускорением 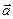в нем понимается ускорение по отношению к инерциальной системе отсчета. Подставив в основное уравнение динамики выражение для абсолютного ускорения, получим:

, (23)

Или

(24)

Стоящие в правой части два последних слагаемых называются силами инерции: переносная сила инерции

(25)

и кориолисова сила инерции

(26)

При введении таких обозначений уравнение движения примет вид:

(27)

и оно будет описывать движение по отношению к неинерциальной системе отсчета.

Таким образом, при описании движения материальной точки по отношению к неинерциальной системе отсчета, к числу действующим на точку активным силам следует добавить две силы инерции - переносную и кориолисову.

Проявление переносной силы инерции ощущает каждый человек, находящийся в движущемся автомобиле, в случае, если автомобиль разгоняется или тормозится, а также на повороте.

Наличие кориолисовой силы инерции из-за вращения Земли проявляется в том, что все движущиеся горизонтально тела в северном полушарии стремятся отклониться вправо по ходу движения, а реки подмывают правый берег, а в южном полушарии наоборот. Поскольку Земля вращается очень медленно, то соответствующие проявления сил инерции следует учитывать лишь при весьма больших скоростях движения точек (скорости снарядов и ракет). При решении обычных технических задач систему отсчета, связанную с Землей, с большой точностью можно считать инерциальной. Для того чтобы система отсчета, движущаяся относительно инерциальной, также была инерциальной, необходимо, чтобы обе силы инерции были равны нулю, следовательно, и оба ускорения (переносное и кориолисово) должны быть нулевыми. Из кинематики известно, что это может быть только тогда, когда подвижная система отсчета движется относительно неподвижной (инерциальной) поступательно, равномерно и прямолинейно.

В случае, когда материальная точка неподвижна в инерциальной системе отсчета, уравнение ее равновесия ( ) будет иметь вид:

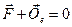. (28)

Это уравнение есть условие относительного покоя материальной точки.

2 ВВЕДЕНИЕ В ДИНАМИКУ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Рассматриваемые вопросы:

Геометрия масс. Центр масс механической системы. Моменты инерции материальной точки относительно полюса, оси, плоскости. Моменты инерции системы материальных точек относительно полюса, оси, плоскости. Моменты инерции абсолютно твердого тела. Моменты инерции однородных тел. Радиус инерции. Физический смысл моментов инерции. Теорема о моментах инерции относительно параллельных осей (теорема Гюйгенса-Штейнера). Полярный и осевые моменты инерции в декартовых координатах, связь между ними. Центробежные моменты инерции. Главные оси инерции и их свойства. Момент инерции относительно оси любого направления. Тензор инерции. Эллипсоид инерции и его физический смысл.

2.1 Механическая система.

Механическая система – это совокупность материальных точек, в которой состояние равновесия или движения отдельных точек зависит от состояния остальных точек.

2.2 Центр масс механической системы.

При рассмотрении движения твердых тел и механических систем, важное значение имеет точка, называемая центром масс.

а) Определение:

Если механическая система состоит из конечного числа материальных точек с массами m₁, m₂, m_n,радиус – векторы которых проведены из одной и той же точки, то центром масс (центром инерции) движущейся механической системы называется геометрическая точка пространства (может быть и вне системы), радиус – вектор которой определяется выражением:

(29)

где: М = - масса механической системы.

Рис. 3

Обозначая декартовы координаты материальных точек (x₁,y₁,z₁), (x₂,y₂,z₂). …, (x_n,y_n,z_n), из (29) проецированием на декартовы оси координат получим следующие формулы для координат центра масс:

 

(30)

 

 

2.3 Моменты инерции материальной точки, механической системы и твердого тела

Было установлено, что масса тела является мерой его инертности. Однако это справедливо только по отношению к поступательному движению, а для вращательного движения мерой инертности будет другая величина. Движение тел существенным образом зависит от характера распределения масс. Например, балерина, группируясь в танце, увеличивает или уменьшает угловую скорость своего вращения. Положение центра масс не характеризует распределения масс. Поэтому при изучении динамики механических систем точек и при изучении динамики твердого тела, вводится еще одна характеристика – момент инерции.

return false">ссылка скрыта

2.3.1 Момент инерции материальной точки.

а) Относительно полюса (точки):

Рис. 4