Вывести дифференциальное уравнение вынужденных колебаний механической системы с одной степенью свободы без учета сопротивления. Изложить его решение в случае отсутствия резонанса.
Q(t) - обобщенная сила характеризующая внешнее воздействие на колебательную систему.
 , где: H - амплитуда, p - циклическая (круговая) частота,
, где: H - амплитуда, p - циклическая (круговая) частота,  - начальная фаза обобщенной силы.
- начальная фаза обобщенной силы.
Определяем положение системы обобщенной координатой q, при равновесии  .
.
Уравнение Лагранжа II рода:  (1).
(1).
Так как равновесие устойчиво, а возмущения малы, для Т и П воспользуемся выражениями:  ,
,  . Находим:
. Находим: 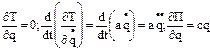 (2).
(2).
Поставляя (2) в (1), получим: 
 , где:
, где: 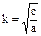 = const, круговая или циклическая частота собственных колебаний системы,
= const, круговая или циклическая частота собственных колебаний системы,  = const.
= const.
 - НЛДУ II порядка с постоянными коэффициентами (1).
- НЛДУ II порядка с постоянными коэффициентами (1).
Решение q(t) это сумма общего решения  однородного уравнения и частного решения
однородного уравнения и частного решения  неоднородного уравнения, то есть:
неоднородного уравнения, то есть:  .
.
Однородное уравнение для определения  это уравнениее собственных колебаний, его решение:
это уравнениее собственных колебаний, его решение:  .
.
Частное решение  неоднородного уравнения называют вынужденными колебаниями системы. Оно зависит от соотношения круговых частот «k» и «p» свободных колебаний и возмущающей силы. Здесь возможны два случая: отсутствие резонанса (
неоднородного уравнения называют вынужденными колебаниями системы. Оно зависит от соотношения круговых частот «k» и «p» свободных колебаний и возмущающей силы. Здесь возможны два случая: отсутствие резонанса (  ) и резонанс (
) и резонанс (  ).
).
k¹p
 - частное решение (1)
- частное решение (1)
Далее, учитывая общее решение уравнения и частное, запишем общее решение для (1):  , или в амплитудной форме:
, или в амплитудной форме:
 .
.
Постоянные 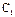 и
и 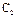 определяются из начальных условий:
определяются из начальных условий: 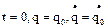 .
.
Вывести дифференциальное уравнение вынужденных колебаний механической системы с одной степенью свободы без учета сопротивления. Изложить его решение в случае резонанса. Графики амплитуды и сдвига фаз вынужденных колебаний.
Q(t) - обобщенная сила характеризующая внешнее воздействие на колебательную систему.
 , где: H - амплитуда, p - циклическая (круговая) частота,
, где: H - амплитуда, p - циклическая (круговая) частота,  - начальная фаза обобщенной силы.
- начальная фаза обобщенной силы.
Определяем положение системы обобщенной координатой q, при равновесии  .
.
Уравнение Лагранжа II рода:  (1).
(1).
Так как равновесие устойчиво, а возмущения малы, для Т и П воспользуемся выражениями:  ,
,  . Находим:
. Находим:  (2).
(2).
Поставляя (2) в (1), получим: 
 , где:
, где: 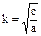 = const, круговая или циклическая частота собственных колебаний системы,
= const, круговая или циклическая частота собственных колебаний системы,  = const.
= const.
 - НЛДУ II порядка с постоянными коэффициентами (1).
- НЛДУ II порядка с постоянными коэффициентами (1).
Решение q(t) это сумма общего решения  однородного уравнения и частного решения
однородного уравнения и частного решения  неоднородного уравнения, то есть:
неоднородного уравнения, то есть:  .
.
Однородное уравнение для определения  это уравнение собственных колебаний, его решение:
это уравнение собственных колебаний, его решение:  .
.
Частное решение  неоднородного уравнения называют вынужденными колебаниями системы. Оно зависит от соотношения круговых частот «k» и «p» свободных колебаний и возмущающей силы. Здесь возможны два случая: отсутствие резонанса (
неоднородного уравнения называют вынужденными колебаниями системы. Оно зависит от соотношения круговых частот «k» и «p» свободных колебаний и возмущающей силы. Здесь возможны два случая: отсутствие резонанса (  ) и резонанс (
) и резонанс (  ).
).
k=p
 - частное решение (1)
- частное решение (1)
Далее, учитывая общее решение уравнения и частное, запишем общее решение для (1):  , или в амплитудной форме:
, или в амплитудной форме:
 .
.
Постоянные 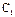 и
и  определяются из начальных условий:
определяются из начальных условий:  .
.
.