Вывести дифференциальное уравнение свободных движений механической системы с одной степенью свободы с учетом сил сопротивления. Изложить его решение в случае малого сопротивления.
Определяем положение системы обобщенной координатой q, при равновесии  .
.
Уравнением Лагранжа II рода:  (1)
(1)
Так как равновесие устойчиво, а возмущения малы, для Т, П и Ф воспользуемся выражениями:  ,
,  ,
,  . Находим:
. Находим: 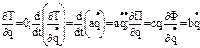 (2).
(2).
Поставляя (2) в (1), получим: 
 , где:
, где:  = const, круговая или циклическая частота собственных колебаний системы без учета сил сопротивления,
= const, круговая или циклическая частота собственных колебаний системы без учета сил сопротивления,  = const, коэффициент затухания. Размерности у «n» и «k» одинаковые (
= const, коэффициент затухания. Размерности у «n» и «k» одинаковые (  ).
).
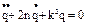 - ОЛДУ II порядка с постоянными коэффициентами.
- ОЛДУ II порядка с постоянными коэффициентами.
Его характеристическое уравнение: 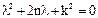

Характер движения системы зависит от соотношения между величинами «n» и «k».
n<k
Случай малого сопротивления. Характеристическое уравнение имеет два различных комплексных корня. Гармонические колебания.

Постоянные A, 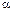 ,
,  и
и  определяются из начальных условий:
определяются из начальных условий: 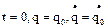 .
.
Вывести дифференциальное уравнение свободных движений механической системы с одной степенью свободы с учетом сил сопротивления. Изложить его решение в случаях критического и большего сопротивления.
Определяем положение системы обобщенной координатой q, при равновесии  .
.
Уравнением Лагранжа II рода: 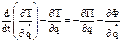 (1)
(1)
Так как равновесие устойчиво, а возмущения малы, для Т, П и Ф воспользуемся выражениями:  ,
,  ,
,  . Находим:
. Находим:  (2).
(2).
Поставляя (2) в (1), получим: 
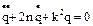 , где:
, где:  = const, круговая или циклическая частота собственных колебаний системы без учета сил сопротивления,
= const, круговая или циклическая частота собственных колебаний системы без учета сил сопротивления,  = const, коэффициент затухания. Размерности у «n» и «k» одинаковые (
= const, коэффициент затухания. Размерности у «n» и «k» одинаковые (  ).
).
 - ОЛДУ II порядка с постоянными коэффициентами.
- ОЛДУ II порядка с постоянными коэффициентами.
Его характеристическое уравнение: 

Характер движения системы зависит от соотношения между величинами «n» и «k».
n=k
Случай критического сопротивления. Характеристическое уравнение имеет два кратных корня. Апериодическое движение.

n>k
Случай большого сопротивления. Характеристическое уравнение имеет два действительных корня. Апериодическое движение.

Постоянные 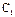 и
и 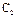 определяются из начальных условий:
определяются из начальных условий: 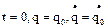 .
.