Операции над множествами

 

Основными являются следующие операции над множествами.

Объединением двух множеств А и В (обозначается A È B) называется множество, состоящее из всех элементов, принадлежащих множеству А или множеству В:

.

Союз «или» здесь неразделительный, т. е. не исключается возможность одновременной принадлежности некоторых элементов обоим множествам. Однако такие элементы зачисляются в объединение только один раз.

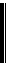Пересечением двух множеств А и В (обозначается А Ç В) называется множество, состоящее из элементов, принадлежащих множеству А и множеству В одновременно:

.

Иными словами, пересечение образовано всеми общими элементами данных множеств.

Разностью двух множеств А и В (обозначается А \ В) называется множество, состоящее из всех элементов А, не входящих в В:

.

Таким образом, из множества А достаточно удалить общие элементы множеств А и В, т. е. все элементы множества А Ç В, чтобы получить разность А \ В.

Симметрической разностью двух множеств А и В (обозначается А ∆ В ) называется множество, состоящее из всех элементов А и В, которые не являются общими для этих множеств.

.

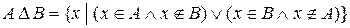Через введённые вышеоперации над множествами симметрическая разность представима следующим образом: А D В = (А È В) \ (А Ç В).

На рисунках 4.3, 4.4, 4.5 и 4.6 заштрихованные множества - это объединение, пересечение, разность и симметрическая разность двух множеств А и В соответственно.

 

Рис. 4.3 Рис. 4.4 Рис. 4.5 Рис. 4.6

Например, если А = {-1, 0, 1, 7, 10, 12} и В = {-6, -4, 0, 1, 3}, то А Ç В = {0, 1}; A È B = {-6, -4, -1, 0, 1, 3, 7, 10, 12}; А \ В = {-1, 7, 10, 12}; A D B = {-6, -4, -1, 3, 7, 10, 12}.

Пусть множество А есть некоторое подмножество множества Е. Тогда множество , состоящее из всех элементов множества Е, не принадлежащих множеству А называется дополнением множества А до множества Е:

.

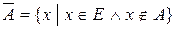Например, если А - множество всех девушек в учебной группе, то дополнением А является множество всех юношей той же группы. Если Е = {х êх – целые числа} и А = {х êх – чётные числа}, то = {х êх – нечётные числа}.

Выбор конкретного способа представления множеств в ЭВМ зависит от целого ряда факторов: особенностей представляемого объекта, состава и относительной частоты использования операций в конкретной задаче и т.д.

Наряду с операциями над множествами, в практической деятельности часто возникает задача рассмотрения отношений между элементами множеств. В частности, отношений упорядочения.

Если a и b – объекты, то записью (a, b) обозначают упорядоченную пару. Равенство упорядоченных пар определяется следующим образом:

(a, b) = (c, d), если a = c и b = d.

В общем случае, (a, b) ¹ (b, a).

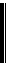Декартовым (или прямым) произведением А ´ В двух множеств А и В называется множество всех упорядоченных пар (a, b), где а Î А, b Î В:

.

Поскольку в определении важен порядок расположения элементов, то пары (а, b) и (b, а), естественно, считаются различными.

В качестве примера рассмотрим два множества А = {1, 2} и В = {4, 7, 8}. Тогда А ´ В = {(1, 4), (1, 7), (1, 8), (2, 4), (2, 7), (2, 8)};

В ´ А = {(4, 1), (4, 2), (7, 1), (7, 2), (8, 1), (8, 2)}.

С помощью декартова произведения можно задать множество точек плоскости. Возьмём прямоугольную систему координат. Тогда каждая точка будет задаваться (упорядоченной) парой чисел (х, у), где х, у Î R, т.е. (x, y) Î R ².

Обобщая рассуждения, можно определить декартово произведение n множеств: А₁ ´ А₂ ´ … ´ А_n - это множество всех (упорядоченных) наборов (a₁, a₂, ... , a_n), где а_i Î А_i при i = l, 2, ... , n. Таким образом в математике возникает n-мерное арифметическое пространство . Если положить п = 3, то с помощью такого произведения будет задаваться пространство трёх измерений. Для этого надо рассмотреть прямоугольную систему координат в пространстве и тогда каждая точка будет определяться тройкой чисел (х, у, z), где х, у, z Î R.