Основные определения, термины и символы
Теория множеств – основа современной математики, оформившаяся как ее самостоятельный раздел в конце XIX века в работах немецкого математика Георга Кантора. Так же, как понятия точки или линии, множество является первичным, интуитивным элементом математики, которое можно описать, но невозможно определить. Поэтому приведем описание этого понятия.
Множество – совокупность различимых между собой объектов, объединяемых в целое некоторым общим признаком. Например, множества: студентов, книг, законов, чисел и т.п.
Обозначения: A, B, C,… – множества, a, b, c,… – элементы (точки) множеств.
Изображение:

| Круги или диаграммы Эйлера - Венна. |
Принадлежность:
aÎ S – элемент a принадлежит множеству S (или входит в S);
aÏ S – элемент а не принадлежит множеству S (или не входит в S).
Задание – два основных способа:
1. Перечисление: А = {3; 8,2; 5}; В = {b1; b2; b9; b7}.
2. Указание характеристического свойства: А = {х| P(x)} – множество А состоит из элементов х, удовлетворяющих свойству Р(х). Например, если в А включаются все точки интервала 1 < х ≤ 2, то запишем: А = {x| 1< х ≤ 2}, т.е. А состоит из элементов х, удовлетворяющих заданному неравенству.
X={x | x*x-5x+6=0} равносильно X={2, 3}
Задание множеств с помощью свойства используется при невозможности задать его перечислением.
При факторном рассмотрении множества могут выделяться его отдельные части. Это называется выделением подмножеств:
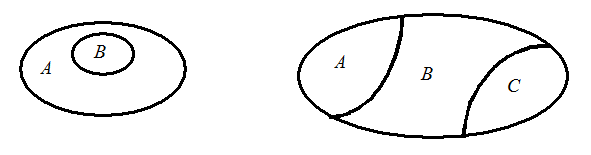
Множество В называется подмножеством множества А, если все элементы В принадлежат и А: В Ì А – В включено (или содержится) в А. Если хотя бы один элемент В не содержится в А, то BË A – В не подмножество (не включено в) А.
Заметим, что при практической работе с каким-то отдельным выбранным подмножеством обычно пользуются термином множество. Так, например, допустимо говорить о множестве книг на одной отдельной полке, хотя они являются подмножеством всех книг на множестве полок в библиотеке.
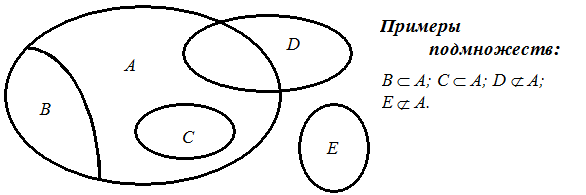
Множество, не содержащее ни одного элемента, называется пустым, обозначается символом Æ и аналогично понятию нуля в арифметике. Оно является подмножеством любого множества. Вообще, множество можно разбить на подмножества самыми разными способами, определяемых необходимостью или личным выбором. Так, из A={3; 8}, можно получить подмножества: Æ, {3}, {8}, {3; 8}.
В={1; 2; 3}, Æ, {1; 2; 3},{1}, {2}, {3}, {1; 2}, { 2; 3}, {1; 3}
Для множества A, содержащего n элементов, число всех возможных подмножеств равно
 .
.