Аналитические показатели динамики
Уровни временного ряда могут изменяться в самых разных направлениях: они могут возрастать и убывать, повторять ранее достигнутый уровень. Интенсивность их изменения бывает различной. Уровни ряда могут изменяться быстрее или медленнее. Для характеристики развития явления во времени применяются следующие показатели:
а) абсолютные приросты △y;
б) темпы роста (Тр);
в) темпы прироста (снижения) (△Тр);
г) абсолютное ускорение или замедление (△");
д) относительное ускорение (△"Тр).
Абсолютное изменение уровней ряда рассчитывается как разность двух уровней. Он показывает, на сколько единиц уровень одного периода больше или меньше уровня другого периода.
В зависимости от базы сравнения абсолютные приросты могут быть цепными и базисными:


Если каждый последующий уровень ряда динамики сравнивается со своим предыдущим уровнем, то прирост называется цепным. Если же в качестве базы сравнения выступает за ряд лет один и тот же период, то прирост называется базисным.
Темп роста- это отношение двух уровней ряда. Как и абсолютные приросты, темпы роста могут рассчитываться как цепные и как базисные:
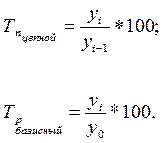
Если база сравнения по периодам меняется, то найденные темпы роста называются цепными. Если же база сравнения по периодам не изменена (у0), то темпы роста называются базисными.
Коэффициент роста-это темпы роста, выраженные в коэффициентах.


В анализе используется один из этих показателей: либо темп роста, либо коэффициент роста, ибо экономическое их содержание одно и то же, по разному выражено: в %(Тр) и в разах (Кр).
Если цепные темпы роста характеризуют интенсивность изменения уровней от года к году (от месяца к месяцу), то базисные темпы роста фиксируют интенсивность роста (снижения) за весь интервал времени между текущим и базисным уровнями.
Темп прироста-это отношение абсолютного прироста к предыдущему уровню динамического ряда (цепной показатель) и к уровню, принятому за базу сравнения по динамическому ряду (базисный показатель):
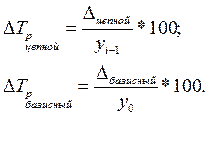
Между цепными и базисными показателями изменения уровней ряда существует следующая взаимосвязь:
а) сумма цепных абсолютных приростов равна базисному приросту;
б) произведение цепных коэффициентов роста равно базисному или равносильное этому деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентам роста;
в) темп прироста связан с темпом роста;
Поэтому при анализе обычно приводится какой то один из них: темп роста либо темп прироста. Зная цепные темпы прироста, можно определить базисный темп прироста. Для этого нужно от темпов прироста перейти к темпам (коэффициентам) роста и далее воспользоваться указанной выше взаимосвязью коэффициентов роста.
Чтобы знать, что скрывается за каждым процентом прироста, рассчитываетсяабсолютное значение 1% прироста как отношение абсолютного прироста за интервал времени к темпу прироста за этот же промежуток времени:

Иными словами,абсолютное значение 1% прироста в данном периоде есть сотая часть достигнутого уровня в предыдущем периоде.
В связи с этим расчет абсолютного значения 1% прироста базисным методом не имеет смысла, ибо для каждого периода это будет одна и та же величина – сотая часть уровня базисного периода.
Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. Если они систематически возрастают, то ряд развивается с ускорением. Величина абсолютного ускорения определяется как
△"=△i -△i-1,
т.е. по аналогии с цепным абсолютным приростом, но сравниваются между собой не уровни ряда, а их скорости.
Если систематически растут цепные темпы роста, то ряд сравнивается с относительным ускорением. Относительное ускорение можно определить как разность следующих друг за другом темпов роста или прироста:

Полученная величина выражается в процентных пунктах.
Относительное ускорение может быть измерено и с помощью коэффициента опережения.
Коэффициент опережения определяется как отношение последующего темпа роста к предыдущему:

Коэффициенты опережения принято рассчитывать в сравнительном анализе нескольких рядов динамики. При параллельном изучении нескольких рядов динамики обычно их приводят к одному основанию путем расчета базисных темпов роста с одинаковой по времени базой сравнения для всех рядов. Это позволяет наглядно видеть, для какого ряда интенсивность изменения уровней наибольшая.