Критерий Вальда
Так как в данном примере aij представляет затраты т.е. потери, то применятся минимаксный критерий.
Для А1: max aij = 24
Для А2: max aij = 28
Для А3: max aij = 23
Для А4: max aij = 27
W = min max aij = 23 Þ наилучшей стратегией развития провозных возможностей в соответствии с минимаксным критерием Вальда будет третья стратегия (А3).
Критерий минимаксного риска Сэвиджа
Для А1: max rij = 11
Для А2: max rij = 13
Для А3: max rij = 17
Для А4: max rij = 21
S = min max rij = 11 Þ наилучшей стратегией развития провозных возможностей в соответствии с критерием Сэвиджа будет первая стратегия (А1).
Критерий пессимизма-оптимизма Гурвица
Положим значение коэффициента пессимизма р = 0,5.
Так как в данном примере aij представляет затраты (потери), то применятся критерий:
HA = min í p min aij + (1-p) max aij ý
| min aij | max aij | p min aij + (1-p) max aij | |
| Для А1 | |||
| Для А2 | 17,5 | ||
| Для А3 | |||
| Для А4 |
Оптимальное решение заключается в выборе стратегии А1
Рассчитаем оптимальную стратегию применительно к матрице рисков
HR = min íp max rij + (1-p) min rijý
| min rij | max rij | p max rij + (1-p) min rij | |
| Для А1 | 5,5 | ||
| Для А2 | 6,5 | ||
| Для А3 | 10,5 | ||
| Для А4 | 10,5 |
Оптимальное решение заключается в выборе стратегии А1
Вывод: в примере предстоит сделать выбор, какое из возможных решений предпочтительнее:
· по критерию Вальда – выбор стратегии А3;
· по критерию Сэвиджа – выбор стратегии А1;
· по критерию
· Гурвица – выбор стратегии А1.
Индивидуальное задание
Решите задачу, согласно вашему индивидуальному варианту.
Вариант 1
Найти наилучшие стратегии по критериям: Вальда, Сэвиджа, Гурвица (коэффициент пессимизма равен 0,2), Гурвица применительно к матрице рисков (коэффициент пессимизма равен 0,4) для следующей платежной матрицы игры с природой (элементы матрицы - выигрыши):
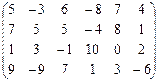
Вариант 2
Дана матрица игры с природой в условиях полной неопределенности (элементы матрицы - выигрыши):
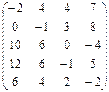
Требуется: проанализировать оптимальные стратегии игрока, используя критерии пессимизма-оптимизма Гурвица применительно к платежной матрице А и матрице рисков R при коэффициенте пессимизма р = 0; 0,5; 1. При этом выделить критерии максимакса, Вальда и Сэвиджа.
Вариант 3
Дана следующая матрица выигрышей:
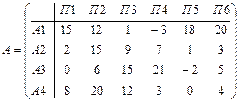
Определите оптимальную стратегию используя критерии Вальда, Сэвиджа и Гурвица (коэффициент пессимизма равен 0,4).
Вариант 4
Один из пяти станков должен быть выбран для изготовления партии изделий, размер которой Q может принимать три значения: 150, 200, 350. Производственные затраты Сi для I станка задаются следующей формулой:
Ci = Pi + ci*Q
Данные Pi и ci приведены в табл4.2.
Таблица 4.2
| Показатели | Модель станка | ||||
| Pi | |||||
| ci |
Решите задачу для каждого из следующих критериев Вальда, Сэвиджа, Гурвица (критерий пессимизма равен 0,6). Полученные решения сравните.
Вариант 5
При выборе стратегии Aj по каждому возможному состоянию природы Si соответствует один результат Vij. Элементы Vij являющиеся мерой потерь при принятии решения, приведены в табл. 4.3.
Таблица 4.3
| Стратегии | Состояние природы | |||
| S1 | S2 | S3 | S4 | |
| A1 | ||||
| A2 | ||||
| A3 |
Выберите оптимальное решение в соответствии с критериями Вальда, Сэвиджа, Гурвица (при коэффициенте пессимизма равном 0,5).
Вариант 6
Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля Rj. Определена экономическая эффективность Vji каждого проекта в зависимости от рентабельности производства. По истечении трех сроков Si рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в табл. 4.4.
Таблица 4.4
| Проекты | Состояние природы | ||
| S1 | S2 | S3 | |
| R1 | |||
| R2 | |||
| R3 | |||
| R4 |
Требуется выбрать лучший проект легкового автомобиля для производства, используя критерий Вальда, Сэвиджа, Гурвица при коэффициенте пессимизма 0,1. Сравнить решения и сделать выводы.
Вариант 7
Определите тип электростанции, которую необходимо построить для удовлетворения энергетических потребностей комплекса крупных промышленных предприятий. Множество возможных стратегий в задаче включает следующие параметры:
R1 – сооружается гидростанция;
R2 – сооружается теплостанция;
R3 – сооружается атомная станция.
Экономическая эффективность сооружения электростанции зависит от влияния случайных факторов, образующих множество состояний природы Si.
Результаты расчета экономической эффективности приведены в табл. 4.5.
Таблица 4.5
| Тип станции | Состояние природы | ||||
| S1 | S2 | S3 | S4 | S5 | |
| R1 | |||||
| R2 | |||||
| R3 |
Вариант 8
Фирма рассматривает вопрос о строительстве станции технического обслуживания (СТО) автомобилей. Составлена смета расходов на строительство станции с различным количеством обслуживаемых автомобилей, а также рассчитан ожидаемый доход в зависимости от удовлетворения прогнозируемого спроса на предлагаемые услуги СТО (прогнозируемое количество обслуженных автомобилей в действительности). В зависимости от принятого решения – проектного количества обслуживаемых автомобилей в сутки (проект СТО) Rj и величины прогнозируемого спроса на услуги СТО – построена в табл. 4.6 ежегодных финансовых результатов (доход д.е.):
Таблица 4.6
| Проекты СТО | Прогнозируемая величина удовлетворяемости спроса | |||||
| -120 | ||||||
| -160 | ||||||
| -210 | -30 | |||||
| -270 | -80 |
Определите наилучший проект СТО с использованием критериев Вальда, Сэвиджа, Гурвица при коэффициенте пессимизма 0,5.
Вариант 9
Магазин может завести один из трех типов товара Аi; их реализация и прибыль магазина зависит от типа товара и состояния спроса. Предполагается, что спрос может иметь три состояния Вi (табл. 4.7). Гарантированная прибыль представлена в матрице прибыли:
Таблица 4.7
| Тип товара | Спрос | ||
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 |
Определить какой товар закупать магазину.
Вариант 10
Дана следующая матрица выигрышей:
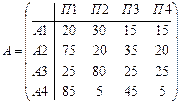
Определите оптимальную стратегию используя критерии Вальда, Сэвиджа и Гурвица (коэффициент пессимизма равен 0,6).
Вариант 11
Администрации театра нужно решить, сколько заказать программок для представлений. Стоимость заказа 200 ф. ст. плюс 30 пенсов за штуку. Программки продаются по 60 пенсов за штуку, и к тому же доход от рекламы составит дополнительные 300 ф. ст. Из прошлого опыта известна посещаемость театра (табл.4.8).
Таблица 4.8
| Посещаемость | |||||
| Ее вероятность | 0,1 | 0,3 | 0,3 | 0,2 | 0,1 |
Ожидается, что 40% зрителей купят программки.
1. Используя критерии Вальда, Сэвиджа и Гурвица, определите, сколько программок должна заказать администрация театра.
2. Допустим, что рекламодатели увеличат сумму с 300 до 400 ф. ст. число посетителей будет больше 5250, к тому же спрос на программки будет полностью удовлетворен. Как это повлияет на рекомендации в п.1?
Вариант 12
При выборе стратегии Aj по каждому возможному состоянию природы Si соответствует один результат Vij. Элементы Vij являющиеся мерой потерь при принятии решения, приведены в таблице:
Таблица 4.9
| Стратегии | Состояние природы | |||
| S1 | S2 | S3 | S4 | |
| A1 | ||||
| A2 | ||||
| A3 |
Выберите оптимальное решение в соответствии с критериями Вальда, Сэвиджа, Гурвица (при коэффициенте пессимизма равном 0,6).
Вариант 13
Пекарня печет хлеб на продажу магазинам. Себестоимость одной булки составляет 30 пенсов, ее продают за 40 пенсов. В табл. 4.10 приведены данные о спросе за последние 50 дней:
Таблица 4.10
| Спрос в день, тыс. шт. | |||||
| Число дней |
Если булка испечена, но не продана, то убытки составят 20 пенсов за штуку. Используя критерии Вальда, Сэвиджа, Гурвица (при коэффициентах: 0,4- вероятность максимальной покупки, 0,6 – вероятность минимальной покупки), определите, сколько булок нужно выпекать в день.
Вариант 14
Компания выбирает, какой вид продукции целесообразно производить. Имеются четыре вида продукции Аj. Определена прибыль от производства каждого вида продукции в зависимости от состояний экономической среды Вi. Значения прибыли для различных видов продукции и состояний природы приведены в табл. 4.11.
Таблица 4.11
| Вид продукции | Состояние экономической среды | ||
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 | |||
| А4 |
Требуется выбрать лучший проект легкового автомобиля для производства, используя критерии Вальда, Сэвиджа, Гурвица при коэффициенте пессимизма 0,4. Сравнить решения и сделать выводы.
Вариант 15
Компания "Kilroy" выпускает очень специфичный безалкогольный напиток, который упаковывается в 40-пинтовые бочки. Напиток готовится в течение недели, и каждый понедельник очередная партия готова к употреблению. Однако в одно из воскресений всю готовую к продаже партию пришлось выбросить. Секретный компонент, используемый для приготовления напитка, покупается в небольшой лаборатории, которая может производить каждую неделю в течение полугода (так налажено производство) только определенное количество этого компонента. Причем он должен быть использован в кратчайший срок.
Переменные затраты на производство одной пинты напитка составляют 70 пенсов, продается оназа 1,50 ф. ст. Однако компания предвидит, что срыв поставок приведет к потере части покупателей в долгосрочной перспективе, а следовательно, придется снизить цену на 30 пенсов. За последние 50 недель каких-либо явных тенденций в спросе выявлено не было (табл. 4.12).
Таблица 4.12
| Спрос на бочки в неделю | |||||
| Число недель |
Определите, что нужно предпринять, используя критерии Вальда, Сэвиджа, Гурвица при коэффициенте пессимизма 0,5. Сравнить решения и сделать выводы.
Контрольные вопросы
1. В чем состоит отличительная особенность принятия решения в игре с «природой»?
2. Специфика мажорирования стратегий в игре с природой?
3. Опишите два способа задания матрицы игры с природой.
4. Что такое величина риска в игре с природой?
5. Опишите критерий Вальда.
6. Опишите критерий Сэвиджа?
7. Опишите критерий Гурвица.
8. Что такое коэффициент пессимизма в критерии Гурвица?
9. В каких критериях используется матрица выигрышей?
10. В каких критериях используется матрица рисков?