Основные принципы и рабочие модели системного анализа

Методы и модели системного анализа (СА) позволяют повысить эффективность разрабатываемых и принимаемых решений – благодаря четкому формированию целей, выделенных учитываемых факторов и условий, их возможной случайности и другой неопределенности, рассматриваемых альтернатив и критериев их отбора, выбираемой программы действий и контроля за их реализацией. При этом оценки выполняются с четким указанием исходных предпосылок и допущений, по - возможности, количественно.

Ключевыми понятиями СА являются: структура, функции, взаимосвязи и взаимодействие системы с над- и подсистемами, развитие системы, модели и методы анализа, критерии.

Существенным свойством эффективной системы является так называемый синергетический (сверхсуммарный) эффект, достигаемый благодаря особому структурно – функциональному взаимодействию элементов системы, при котором ее свойства принципиально отличаются от свойств ее частей; (элементарный пример: свойство управляемо летать присуще лишь летательному аппарату в целом, но не отдельным его частям).

Первый шаг СА – представить исследуемый объект (продукт или процесс, в том числе информационный) в виде системы, для чего необходимо выявить и четко определить структуру системы (элементы системы, с их устойчивыми связями и взаимодействиями), под- и надсистемы, главную полезную функцию (ГПФ) системы. Исследование системы рекомендуется проводить по следующим трем направлениям, дополняющим друг друга:

а. предметно – структурный анализ должен дать ответ на вопрос о необходимых и достаточных элементах системы и их связях о надсистеме;

б. функциональный анализ проясняет внутренние и внешние функции системы, т.е. как работает каждый компонент в системе, как система работает в надсистеме;

в. анализ развития – определение стадий жизненного цикла системы, выявление текущего состояния, и прогнозные оценки вариантов дальнейшего развития.

На практике нередко возникают трудности правильного выявления надсистемы. Есть следующее практическое правило: задать себе контрольный вопрос «Зачем эта система, что она должна делать?», ответ на него помогает определить ГПФ системы; следующий вопрос «для чего нужна эта ГПФ?», вот эта «надфункция» и выявляет надсистему (возможно не одну).

Основополагающим принципом СА является программно – целевой подход (ПЦП).

В чем его главное отличие от привычного, традиционного подхода?

В последнем планирование ведется исходя из «внутренней» информации, «от достигнутого уровня», траектория движения системы – обычно продолжение предыдущего, часто под флагом лозунгов типа «максимальный рост выпуска продукции», или даже явная бессмыслица «максимум продукции при минимуме затрат». Суть ПЦП предельно компактно, но достаточно емко можно представить в виде аббревиатуры:

ЦИПо Кр Ре Мо С Пр Ме К,

которая отражает влияние 10 ключевых факторов, условий эффективности:

«Цели – Измерители (вехи) – Последствия – Критерии – Ресурсы – Модели – Совместимость – Программа – Механизм - Контроль».

Цели следует выбирать с учетом требований надсистемы. Количественные «измерители» (вехи) необходимы для объективизации продвижения к цели. Обязателен учет возможных последствий (как положительных, так и отрицательных). Варианты программы разрабатывают, сравнивают и оптимизируют по заданной совокупности критериев, с обязательным учетом располагаемых и намечаемых ресурсов, на основе моделирования жизненного цикла системы, оценивая при этом фактор совместимости (чтобы исключить нередко встречающуюся несовместимость «старого» и «нового», предусмотреть необходимые сопряжение и адаптацию). Программа определяет этапы, что и когда конкретно делать, требуемые для этого взаимосвязи. Механизм же фиксирует необходимые средства, технологию реализации программы, ее исполнителей. Наконец, контроль – не пассивная регистрация хода событий, а активный управляемый процесс, предполагающий при необходимости коррекцию программы.

ПЦП следует применять не только при крупномасштабных, наукоемких, дорогостоящих НИОКР, но, например, при выборе стратегии развития фирмы, при разработке бизнес – плана, маркетингового исследования, реорганизации управления фирмой.

При формировании критериев на практике обычно сталкиваются с проблемой многокритериальности: как увязать часто противоречивые требования к оптимизируемым параметрам системы и условиям ее функционирования; причем, критерии разной природы имеют различные единицы измерения, а у некоторых вообще нет естественной шкалы измерения. Для наглядной увязки группы критериев можно использовать диаграмму «паутина», имеющую следующий вид (рис. 5), где каждому из критериев соответствует радиус, на котором указана соответствующая шкала измерения (естественная или условная, задаваемая в баллах); причем, направление шкалы выбирают таким, чтобы в центре круга было максимально благоприятное численное значение критерия:

К₄

К₁

К₃ К₂

Рис. 6

Таким образом, имея для конкретного варианта системы численные значения каждого из критериев, фиксируя их на радиусах – шкалах, а затем соединяя эти точки, получают «паутину». Два варианта системы сравнивают по картине их паутин: чем оптимальнее система, тем более паутина стянута к центру. Однако диаграмма «паутина» не позволяет формализовать учет различной значимости критериев, их больший или меньший вклад в результат выбора варианта системы.

В научно – методической литературе рассмотрено немало методов «свертки» критериев – переходу от группы частных, разнородных критериев к одному, обобщенному. В последние годы значительный интерес специалистов – практиков в различных областях привлек метод обобщенной функции Харрингтона, логика и процедура применения которого вкратце следующие.

Вначале шкалы измерения каждого критерия преобразуют – переходя к безразмерной, с диапазоном от 0 до 1 (1 соответствует предельно благоприятной величине критерия, 0 – предельно неблагоприятной).

Такой переход можно осуществить или с помощью специально разработанных таблиц, или графически (последний вариант как наиболее наглядный, легче пояснить):

f₁f₂

O К₁O К₂

Рис. 7

Пусть, например, критерий К₁ - прогнозируемый срок разработки, а К₂ - ожидаемая прибыль, f₁ и f₂ – частные функции полезности, соответственно для К₁ и К₂. Очевидно стремление К₁ – min, К₂– max, чему соответствует характер зависимостей f₁(К₁) и f₂(К₂), выбираемых экспертно с учетом относительного вклада каждого критерия в комплексную эффективность системы: при К₁→ min f₁→ 1, при К₂→ max f₂→ 1. Таким образом, в идеале желательно одновременно достичь f₁= f₂ =1. Так как все частные функции полезности fi безразмерны и измеряются по одной и той же шкале [0,1], то логично перейти к обощенной функции полезности F, построив ее в виде среднего геометрического от fi

F= ,

при этом величина F, как и f_i; безразмерна и измеряется в интервале [0,1]. Имея вариант системы А с численными значениями критериев 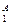(К , К 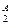) и вариант Б с К , К 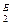…, а затем переходя от частных критериев к их частным функциям полезности (т.е. K_i→f_i), а далее к обобщенной функции полезности F для каждого из сравниваемых вариантов системы, получаем F и F 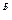; этот метод позволяет сопоставить варианты не только по величине обобщенного критерия F, но и проследить относительный вклад каждого частного критерия.