Общая форма таблицы сопряженности размерности 2x2

 

Переменная Y	Переменная X
		Всего
	А	b	a + b
	С	d	c + d
Всего	а + с	b + d	N

 

Предположим, мы располагаем таблицей сопряженности для двух переменных-признаков X и Y, каждая из которых принимает лишь два значения, которые мы условно обозначим как «0» и «1». В каждой из четырех клеток таблицы содер­жатся абсолютные частоты, т. е. число случаев для каждого из возможных соче­таний значений признаков (т. е. для сочетаний «0—1», «1—1», «0—0», «1—0»). Обозначим частоты в каждой из клеток таблицы латинскими буквами а, b, с и d. В такой общей форме таблица сопряженности для двух дихотомических при­знаков будет выглядеть как на таблице 8.4.

Для расчета коэффициента сопряженности «фи» используют формулу:

 

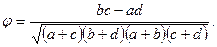
Эта простая в вычислительном отношении формула получается в результате ряда преобразований исходной формулы для вычисления величины «хи-квад­рат» (c²). Эта исходная формула позволяет лучше понять общую идею оценки связи качественных признаков, которую мы опишем, не вдаваясь в статисти­ческие детали. Исходная формула для величины «хи-квадрат» выглядит так:

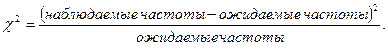
Понятно, что наблюдаемые частоты мы можем найти в клетках таблицы сопря­женности. Но что понимается под ожидаемыми, точнее, теоретически ожидае­мыми частотами? Ожидаемые частоты — это те частоты, которые должны были бы стоять в клетках той же таблицы сопряженности, если бы две интересую­щие нас переменные были бы независимы, т. е. расслоение наблюдений по од­ному признаку оставалось бы пропорциональным для разных подгрупп, выде­ленных по другому признаку.

Пусть, например, данные относительно участия в парламентских выборах для 1000 опрошенных позволили построить таблицу 8.5.

Таблица 8.5