Вычисление среднего возраста посетителей библиотеки

 

Возраст	абсолютная частота, fi	Xi x fi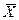
18	5	90	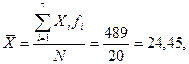(где i = 1...7 — число различных значений)
19	2	38
21	4	84
22	6	132
30	1	30
35	1	35
80	1	80
	Всего

 

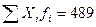
Среднее обладает рядом важных свойств. В частности, если сложить все значения отклонений от среднего значения, т. е. разности между X и X₁ X₂ ... X_i(которые могут быть и положительными, и отрицательными), то сумма отклонений будет равна нулю. Кроме того, сумма квадратов отклонений наблюдаемых значений от их арифметического среднего меньше суммы квадратов отклонений от любой другой точки[193]. Эти свойства среднего определяют его уникальную роль в решении ряда статистических задач, о кото­рых мы будем говорить ниже. Сейчас достаточно отметить то обстоятельство, что при использовании среднего в качестве «представителя» (т. е. статистичес­кой оценки) каждого из наблюдаемых значений, ошибка, определяемая как сумма квадратов отклонений, будет минимальной. Не стоит, однако, забывать о том, что и минимальная ошибка может быть достаточно большой. Так, для малых выборок, имеющих более чем одну моду, любая мера центральной тенденции, включая среднее, будет недостаточно хороша. Центральной тенденции в таком распределении просто не существует.

Выбирая меру центральной тенденции, нужно руководствоваться знанием ее свойств, общей формой распределения и, наконец, здравым смыслом. Если при взгляде на гистограмму исследователь обнаруживает, что имеет дело сунимо­дальным симметричным распределением (половины гистограммы слева и справа от модального значения зеркально совпадают), то среднее, медиана и мода бу­дут равны между собой. Если речь идет о выборке из большой совокупности, где интересующая исследователя переменная-признак распределена нормаль­но (т.е. большие и малые крайние значения встречаются редко, а средние — часто), наилучшим показателем будет среднее. Если в унимодальном распреде­лении встречаются крайние значения, могущие значительно повлиять на сред­нее (см. пример с возрастом, табл. 8.2), нужно отдать предпочтение медиане.

Вопрос о сравнимости средних значений не так тривиален, как это может пока­заться. Сравнение значений средних показателей для различных выборок или для одной и той же выборки в разные моменты времени — весьма распростра­ненный способ анализа результатов. Не только в научных журналах, но и в газе­тах мы постоянно находим сведения о сравнительной величине душевого дохо­да в разных регионах, о различиях в среднем числе автомобилей, приходящих­ся на одну семью и т. п. Следует, однако, помнить о том, что заведомо некорректны сравнения различных мер центральной тенденции, например ме­дианы и среднего. Причина здесь в том, что различные меры описывают раз­ные характеристики распределения: медиана — среднее положение, мода — са­мое часто встречающееся значение и т. д. Кроме того, даже две одинаковые меры центральной тенденции не всегда сравнимы. Средние двух распределе­ний имеет смысл сравнивать лишь в том случае, если во всех других отношени­ях распределения одинаковы, имеют сходную форму. Если исследователь говорит о равенстве средних значений, забыв упомянуть о том, что одно распреде­ление симметрично, а другое — скошено вправо или влево из-за присутствия очень больших либо очень малых значений в его «хвостовых» частях, то он подталкивает читателя к заведомо неверному выводу о том, что анализируемая переменная распределена в двух выборках совершенно одинаково. Среднее рас­пределения с очень длинным правым «хвостом» может оказаться равным сред­нему распределения, скошенного влево, где встречаются крайне малые значе­ния признака. Но этим сходство будет исчерпываться: что общего (кроме вели­чины среднего) у группы, включающей много людей с очень низким доходом, коэффициентом интеллекта и т. п., с другой группой, включающей много на­блюдений с очень высокими значениями переменной-признака?

Очевидно, важно не только знать, что типично для выборки наблюдений, но и установить, насколько выражены отклонения от типичных значений. Чтобы определить, насколько хорошо та или иная мера центральной тенденции опи­сывает распределение, нужно воспользоваться какой-либо мерой изменчивос­ти, разброса.

Самая грубая мера изменчивости — размах (диапазон) значений. Эта мера не учитывает индивидуальные отклонения значений, описывая лишь диапазон их изменчивости. Под размахом понимают разность между максимальным и ми­нимальным наблюдаемым значением. Если количество карманных денег в груп­пе из десяти субъектов варьирует от 100 рубл. (1 человек) до 100000 рубл. (2 человека), размах будет равен 100000-100 = 99900.

Еще одна грубая мера разброса значений — это коэффициент вариации (V), который определяется просто как процент наблюдений, лежащих вне модаль­ного интервала, т. е. процент (доля) наблюдений, не совпадающих с модальным значением. Если от модального отличаются 60% значений, то V = 60% (или V = 0,6).

Рассказывая о процедуре построения шкалы Терстоуна, мы описали, как вычислить междуквартилъный размах — очень удобный показа­тель разброса значений для ординальной переменной. Напомним, что нижний, первый, квартиль (Q₁) отсекает 25% наблюдений, а ниже третьего квартиля (Q₃) лежат уже 75% случаев. Полумеждуквартилъный размах равен половине рас­стояния между третьим и первым квартилями:

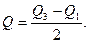
Если распределение приблизительно симметрично, то можно считать, что полумеждуквартильный размах указывает границы, в которых лежит 50% дан­ных по обе стороны медианы или среднего.

Все эти меры изменчивости, как уже говорилось, можно считать скорее грубы­ми и приблизительными. Ни одна из них не уделяет должного внимания инфор­мации об отклонениях каждого отдельного наблюдаемого значения от средне­го, хотя эта информация в большинстве случаев может быть получена из анали­за распределения. Информацию о вариации некоторой совокупности значений относительно среднего несут значения отклонений от среднего, о которых мы уже говорили. Однако, просуммировав все значения отклонения ( 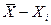), мы получим нуль. Положительные и отрицательные отклонения будут взаимоуничтожаться. Если же мы возведем в квадрат каждое отклонение и просуммируем квадраты отклонений, то мы получим хорошую меру рассеяния, которая будет маленькой, когда данные однородны, и большой, когда данные неоднородны. Чтобы суммы квадратов отклонений для выборок разного размера можно было сравнивать, нужно поделить каждую из них на N, где N— объем выборки[194].

 

 

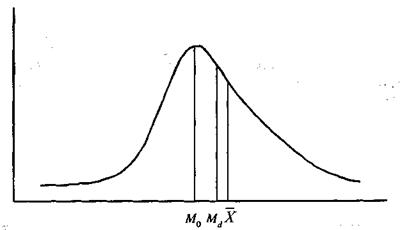
Рис. 17.Распределение, скошенное вправо

 

Именно так и получают важнейшую меру рассеяния — дисперсию (s²). Если 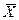— среднее, X₁, Х₂... Х_п — индивидуальные значения измеряемой переменной X в данной совокупности, а N — объем выборки[195]:

 

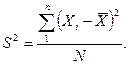
Для того чтобы вычислить значение дисперсии, нужно вычесть из каждого наблюдаемого значения среднее, возвести в квадрат все полученные откло­нения, сложить квадраты отклонений и разделить полученную сумму на объем выборки.