Средняя геометрическая

Если имеется n коэффициентов роста, то формула среднего коэффициента:

Если осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Например, с помощью средней квадратической можно определить диаметры труб, колес и т. д.

Средняя квадратическая простая определяется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число.

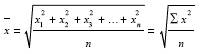
Средняя квадратическая взвешенная равна:

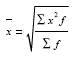
37. Как исчисляется средняя арифметическая простая и в каких случаях она применяется?

Один из наиболее распространенных видов средней – средняя арифметическая,которая исчисляется тогда, когда объем ос–редняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.

Для вычисления средней арифметической величины сумму всех уровней признака делят на их число.

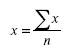
38. Как исчисляется средняя арифметическая взвешенная и в каких случаях она применяется?

Если некоторые варианты встречаются несколько раз, то сумму уровней признака можно получить умножением каждого уровня на соответствующее число единиц совокупности с последующим сложением полученных произведений, исчисленная таким образом средняя арифметическая называется средней арифметической взвешенной.

Формула средней арифметической взвешенной выглядит следующим образом:

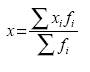
гдех_i – варианты,

f_i – частоты или веса.

Взвешенная средняя величина должна употребляться во всех случаях, когда варианты имеют различную численность.

39. Каковы основные свойства средней арифметической?

Для снижения трудоемкости расчетов используются основные свойства ср.арифм-кой:

1.Если все варианты усредняемого признака увеличить/уменьшить на постоянную величину А, то средняя арифметическая соответственно увеличится/уменьшится.

2.Если все варианты, определяемого признака увеличить/уменьшить в н-раз, то ср.арифм увеличится/уменьшится в н-раз.

3.Если все частоты усредняемого признака увеличить/уменьшить в постоянное число раз, то ср.арифм.останется неизменной.

40. Для чего служит средняя гармоническая? Чем она отличается от средней арифметической?

Средняя гармоническая величина является модифицированной формой средней арифметической. Она применяется в тех случаях, когда неизвестны значения частот у вариантов ряда, зато имеются для каждого произведения этих вариант на соответствующие им частоты.

Средняя гармоническая

Средняя геометрическая используется для расчета среднего коэффициента или темпа роста статистического показателя

41. Что предоставляет собой линейное отклонение, его формулы; в чем его недостатки показателя вариации?

Среднее линейное отклонение ( 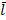) – представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитываются невзвешенное среднее линейное отклонение.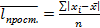

Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейной отклонений, где весами выступают частоты соответствующих вариант:

Однако и этот показатель вариации имеет существенные недостатки Основным является то, что в нем не учитываются знаки (направленность) отклонений Произвольное отвержение алгебраических знаков отклоненный Приводит к тому, что математические свойства этого показателя далеко не элементарными, а это Значительно усложняет использование среднего линейного отклонения при решении задач, связанных с вероятными расчетами Поэтому среднее линейное отклонение употребляется редкий.

42. Какой показатель вариации называется дисперсией? По каким формулам она рассчитывается?

Дисперсией ( ) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней:

Для не сгруппированных данных:

Для сгруппированных данных:

43. Что называется средним квадратическим отклонением? По каким формулам оно вычисляется

Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением)

Для несгруппированных данных: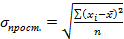

Для сгруппированным данных: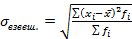

44. Коэффициент вариации как показатель, формула его вычисления и значение для экономического анализа.

Для сравнения вариаций одного и того же показателя в разных совокупностях (например, заработной платы двух фирм) или вариации различных показателей в одной совокупности (например, вариации заработной платы и возраста внутри одной фирмы) используют относительные показатели вариации. К ним относят:

Коэффициент осцилляции: ;

Относительное линейное отклонение: ;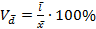

Коэффициент вариации: ;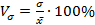

Принято считать, что если значение коэффициента вариации больше 33%, то совокупность неоднородна и для дальнейшего статистического анализа следует либо исключить крайние значения признака, либо разбить совокупность на однородные группы (требование однородности данных присутствует практически во вех видах статистического анализа).

45. Что такое мода?

Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.

Мода (Мо) – чаще всего встречающийся вариант.

Мода (Мо) –это наиболее часто встречающееся значение признака, или иначе говоря, значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по-разному.

Для интервального ряда:

где нижняя граница модального интервала;

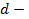величина интервала;

частота модального интервала;

частота интервала, предшествующего модальному;

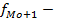частота интервала, следующего за модальным.

Для дискретных рядов распределения модой является значение признака, которому соответствует наибольшая частота.

Мода зависит от величины групп, от точного положения границ групп.

Определить модальное значение признака можно и по графику. Для этого в случае дискретных вариационных рядов строится полигон распределения. Значение абсциссы, соответствующее наибольшей вершине полигона, будет значением моды.

Если имеется интервальный вариационный ряд с равными интервалами, то для определения моды строится гистограмма, у которой на оси абсцисс находятся значения границ интервалов, а на оси ординат – соответствующие интервалам частоты. На гистограмме модальный интервал будет иметь наибольшую высоту столбца. Затем надо провести линии, соединяющие вершины модального столбца с прилегающими вершинами соседних столбцов. Для нахождения значения моды из точки пересечения проведенных линий на ось абсцисс опускается перпендикуляр. Абсцисса точки пересечения будет значением моды.

46. Что такое медиана?

Медиана (Me)– это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.

Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения.

Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.

Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.

Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал.

Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.

Для определения медианы в интервальном ряду сначала находится медианный интервал. Для этого находится порядковый номер медианы 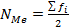. Накопленная частота, которая равна номеру медианы или первая его превышает, в интервальном вариационном ряду соответствует медианный интервал.

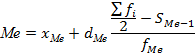
где 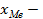нижняя граница медианного интервала;

величина медианного интервала;

накопленная частота интервала, предшествующего медианному;

частота медианного интервала.

47. Для чего нужно изучать динамику явлений?

Ряды динамики используются для отражения развития экономических явлений и процессов при переходе от одного момента времени к другому.

Динамическими рядами в статистической науке называют статистические данные, характеризующие изменения явлений во времени, они строятся для выявления и изучения возникающих закономерностей в развитии явлений в различных сферах жизни общества.

48. Дайте определение ряда динамики. Из каких элементов он состоит и каков их смысл?

В рядах динамики имеются два главных элемента:

1) показатель времени (t);

2) уровни развития изучаемого явления (у).

В рядах динамики в качестве показателей времени могут выступать определенные даты времени или отдельные периоды.

Уровни, образующие ряды динамики, определяют количественную оценку развития во времени исследуемого явления или процесса, они могут выражаться относительными, абсолютными либо средними величинами. Уровни рядов динамики в зависимости от характера исследуемого явления могут относиться к определенным датам времени или к отдельным периодам.

49. Какие виды рядов динамики существуют?

Ряды динамики подразделяются на моментные, интервальные и ряды средних величин.

Моментные ряды динамики отображают состояние исследуемых процессов на определенные даты времени.

Интервальные ряды динамики отображают итоги развития или функционирования исследуемых процессов за отдельные периоды времени.

Для характеристики процесса за определенный период рассчитывают средний уровень из всех членов динамического ряда.

50. Каковы правила построения рядов динамики?

При построении динамических рядов необходимо соблюдать определенные правила: основным условием для получения правильных выводов при анализе рядов динамики и прогнозировании его уровней является сопоставимость уровней динамического ряда между собой. [1 стр. 110]

1. Периодизация развития, т. е. расчленение его во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. Это, по существу, типологическая группировка во времени.