Виды сводки
Различают простую и сложную сводку:
§ При простой сводке производится подсчет общих итогов по изучаемой совокупности.
§ При сложной сводке производится группировка единиц наблюдения, подсчет итогов по каждой группе и по всей совокупности, и представление результатов группировки в виде статистических таблиц.
13. Что называется статистической группировкой и группировочными признаками?
Группировка — это метод, при котором вся исследуемая совокупность разделяется на группы по какому-то существенному признаку.
Признак, по которому осуществляется группировка называется группировочным признаком или основанием группировки.
14. В чем сложность выбора группировочного признака?
Выбор группировочного признака зависит от характера изучаемых явлений и целей группировки. Признак, который служит основанием для распределения явлений по группам, называется группировочным признаком.Важнейший вопрос группировки – оптимальный выбор группировочного признака. Признак должен быть существенным, а не второстепенным или малозначительным.
При выборе группировочных признаков необходимо также сообразовываться и с тем, что одни и те же признаки могут иметь различные значения в зависимости от конкретных условий, места и времени. Поэтому с изменением в развитии изучаемого явления видоизменяются приемы группировки, берутся другие группировочные признаки.
15. Какие задачи решает статистика при помощи метода группировок?
Статистические группировки – первый этап статистической сводки, позволяющий выделить из массы исходного статистического материала однородные группы единиц, обладающих общим сходством в качественном и количественном отношениях. Важно понимать, что группировка – это не субъективный технический прием разделения совокупности на части, а научно обоснованный процесс разделения множества единиц совокупности по определенному признаку.
Основополагающим принципом применения метода группировок является всесторонний, глубокий анализ сущности и природы изучаемого явления, позволяющий определить его типические свойства и внутренние различия.
16. Дайте характеристику типологических, структурных и аналитических группировок. Какие задачи они решают?
Типологическая группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей).
Структурная дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги.
Аналитическая (факторная) группировка позволяет оценивать связи между взаимодействующими признаками.
17. В чем выражается взаимосвязь вышеуказанных группировок?
Содержание и приемы группировок многообразны. Различны и задачи, выполняемые ими. Однако принято выделять следующие основные задачи, решаемые с помощью метода статистических группировок: образование социально-экономических типов явлений; изучение строения изучаемых явлений и структурных изменений, происходящих в них; выявление связи между изучаемыми признаками.
Для решения этих задач соответственно применяют типологические структурные и аналитические группировки. Следует отметить, что приведенная классификация статистических группировок по выполняемым ими задачам имеет некоторую условность, поскольку они на практике применяются в комплексе. Это обусловлено многогранностью процессов, протекающих в общественной жизни, в том числе и в коммерческой деятельности.
18. Какие группировки называют простыми и сложными и в чем преимущество последних?
Виды группировок по числу группировочных признаков:
· простая – (один признак)
· сложная-( два и более признаков); (комбинационная, многомерная)
Образование групп по двум и более признакам (2-4), взятым в определенном сочетании, называется комбинационнойгруппировкой. Многомерная - любое число признаков свыше четырех.
Принцип построения комбинационной группировки заключается в том, что сначала группы формируется по одному признаку, затем они делятся на подгруппы по другому признаку, а эти, в свою очередь, делятся по третьему и т.д. При этом группировочных признаки принято располагать, начиная с атрибутивного, в определенной последовательности, исходя из логики взаимосвязи показателей.
Применение сложных группировок обусловлено многообразием экономических явлений, а также необходимостью их всестороннего изучения. Но увеличение числа группировочных признаков ограничивается уменьшением наглядности, что снижает эффективность использования статистической информации.
19. От чего зависит решение вопроса об определение числа групп и границ интервалов между ними?
Количество групп и величина интервала связаны между собой: чем больше образовано групп, тем меньше интервал, и наоборот. Количество групп зависит от числа единиц исследуемого объекта и степени колеблемости группировочного признака. При небольшом объеме совокупности нельзя образовывать большое число групп, так как группы будут малочисленными.
20. Какие бывают интервалы группировок и как точно обозначить их границы? Приведите примеры.
Интервалы могут быть равные и неравные. При исследовании экономических явлений могут применяться неравные (прогрессивно возрастающие, прогрессивно убывающие) интервалы. Так, например, по численности работающих промышленные предприятия могут быть разбиты на следующие группы: до 100 человек, 100-200, 200-300, 300-500, 500-1000, 1000 и более человек. Это объясняется тем, что количественные изменения размера признака имеют не одинаковые значения в низших и высших по размеру признака группах: изменение количества работающих на 50-100 человек имеет существенное значение для мелких предприятий, а для крупных - не имеет.
21. Что называется вторичной группировкой, в каких случаях приходится прибегать к ней и как можно получить новые группы на основании уже имеющихся?
Вторичная группировка - образование новых групп на основе ранее осуществленной группировки.
Получение новых групп на основе имеющихся возможно двумя способами перегруппировки: объединение первоначальных интервалов (путем их укрупнения) и долевой перегруппировкой (на основе закрепления за каждой группой определенной доли единиц совокупности).
22. Что называется статистической таблицей? Каковы основные элементы статистической таблицы? В чём отличие простых и сложных таблиц?
Статическая таблица- форма наиболее рационального изложения полученных в результате статистической сводки и группировки числовых (цифровых) данных По внешнему виду она представляет собой комбинацию вертикальных и горизонтальных строк, содержащую боковые и верхние заголовки. Статистическая таблица содержит подлежащее и сказуемое.
Подлежащее таблицы представляет ту статистическую совокупность, о которой идет речь в таблице, т. е. перечень отдельных или всех единиц совокупности либо их групп. Чаще всего подлежащее помещается в левой части таблицы и содержит перечень строк.
Сказуемое таблицы- показатели, с помощью которых дается характеристика явления, отображаемого в таблице.
Если в подлежащем таблицы содержится простой перечень каких-либо объектов, таблица называется простой. В подлежащем простой таблицы нет каких-либо группировок статистических данных. Если подлежащее простой таблицы содержит перечень территорий, то такая таблица называетсятерриториальной.
Простая таблица содержит только описательные сведения, ее аналитические возможности ограничены. Глубокий анализ исследуемой совокупности, взаимосвязей признаков предполагает построение более сложных таблиц - групповых и комбинационных.
Групповые таблицысодержат в подлежащем группировку единиц объекта наблюдения по одному существенному признаку. Простейшим видом групповой таблицы являются таблицы, в которых представлены ряды распределения. Групповая таблица может быть более сложной, если в сказуемом приводится не только число единиц в каждой группе, но и ряд других важных показателей, количественно и качественно характеризующих группы подлежащего. Такие таблицы часто используются в целях сопоставления обобщающих показателей по группам, что позволяет сделать определенные практические выводы.
23. Каково назначение графического представления статистических данных? Виды графиков.
Главное достоинство статистических графиков - наглядность. Диаграммы - наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и способы их построения разнообразны. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т. д. При этом сравнение исследуемых совокупностей производится по какому-либо существенному варьирующему признаку.
Статистические карты - графики количественного распределения по поверхности. По своей основной цели они близко примыкают к диаграммам и специфичны лишь в том отношении, что представляют собой условные изображения статистических данных на контурной географической карте, т. е. показывают пространственное размещение или пространственную распространенность статистических данных.
24. Что такое абсолютные статистические величины и каково их значение? Приведите примеры абсолютных величин.
Статистические данные, полученные при наблюдении, в результате сводки, группировки, почти всегда являются абсолютными величинами, т. е. величинами, которые выражены в натуральных единицах и получены в результате счета или непосредственного измерения. Абсолютные величины отражают численность единиц изучаемых совокупностей, размеры или уровни признаков, зарегистрированных у отдельных единиц совокупности, и общий объем количественно выраженного признака как результат суммирования всех его отдельных значений.
Абсолютные величины имеют большое познавательное значение.
например, срок службы сооружения или какого-либо изделия, продолжительность горения лампочки (в часах), средняя продолжительность жизни человека (в годах) и др.
25. Назовите виды статистических показателей. Приведите примеры.
Выделяют два вида статистических показателей:
.Конкретный статистический показатель
.Показатель категория.
Конкретный статистический показатель характеризует размер, величину изучаемого явления или процесса в данном месте и в данное время (под привязкой к месту понимается отношение показателя к какой-либо территории или объекту). Так, если мы называем конкретную величину стоимости промышленно производственных фондов, то обязательно должны указать, к какому предприятию или отрасли и какому моменту времени она относится.
Показатель-категория отражает сущность, общие отличительные свойства конкретных статистических показателей одного и того же вида без указания места, времени и числового значения. Например, показатели розничного товарооборота предприятий торговли и общественного питания в Минске и Витебске в 2000 и 2004 гг. отличаются местом, временем и конкретными числовыми значениями, но имеют одну и ту же сущность (продажа товаров через розничную торговую сеть и сеть предприятий общественного питания), которая отражена в показателе-категории «Розничный товарооборот предприятий торговли и общественного питания».
26. В каких единицах измерения выражаются абсолютные статистические величины? Приведите примеры.
Единицы измерения абсолютных величин отражают свойства единиц статистической совокупности и могут бытьпростыми, отражая 1 свойство (например, масса груза измеряется в тоннах) или сложными, отражая несколько взаимосвязанных свойств (например, тонно-километр или киловатт-час).
27. Всегда ли для изучаемого явления достаточно одних абсолютных показателей?
Одних абсолютных статистических величин недостаточно для характеристики изучаемых объектов. Чтобы отразить состояние, рост, развитие явлений, соотношение их во времени и пространстве, в статистике широко пользуются относительными величинами.
28. Что называется относительными величинами?
Относительные величины дают представление, во сколько раз одна абсолютная величина больше другой или какую часть одна абсолютная величина составляет от другой, или сколько единиц одной совокупности приходится на единицу другой.
Относительные величины – это показатель, который представляет собой частное от деления двух статистических величин и характеризует количественное соотношение между ними.
29. Каковы основные условия правильного расчета относительной величины?
Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Таким образом, по способу получения относительные показатели – всегда величины производные, определяемые в форме коэффициентов, процентов, промилле, продецимилле и т.п. Однако нужно помнить, что этим безразмерным по форме показателям может быть, в сущности, приписана конкретная, и иногда довольно сложная, единица измерения. Так, например, относительные показатели естественного движения населения, такие как коэффициенты рождаемости или смертности, исчисляемые в промилле (‰), показывают число родившихся или умерших за год в расчете на 1 000 человек среднегодовой численности; относительная величина эффективности использования рабочего времени – это количество продукции в расчете на один отработанный человеко-час и т.д.
30. В какой форме могут быть относительные величины? От чего она зависит?
Форма выражения зависит от: количественного соотношения сравниваемых величин; смыслового содержания полученного результата сравнения. Если сравниваемый показатель больше основания, тогда относительная величина выражается в коэффициенте или в проценте, но если сравниваемый показатель меньше основания, тогда относительную величину лучше выразить только в проценте.
31. Какие виды относительных величин вы знаете? Приведите примеры.
1. Относительная величина выполнения договорных обязательств– это показатель, характеризующий уровень выполнения предприятием своих обязательств, предусмотренных в договорах. Расчет показателя производится путем соотношения объема фактически выполненных обязательств и объема обязательств, предусмотренных в договоре. Выражается он в форме коэффициентов или в процентах.
2. Относительные величины структуры– это показатели, характеризующие долю от состава изучаемых совокупностей. Относительная величина структуры определяется отношением абсолютной величины отдельного элемента статистической совокупности к абсолютной величине всей совокупности, т. е. как отношение части к общему (целому), и характеризует удельный вес части в целом, в форме процента. В анализе коммерческой деятельности торговли и сферы услуг относительные величины дают возможность изучить весь состав товарооборота по его ассортименту, состав работников фирмы – по определенным признакам (стажу работы, полу, возрасту), состав расходов предприятия и другие факторы, влияющие на коммерческую деятельность предприятия.
3. Относительные величины динамикихарактеризуют изменение изучаемого явления во времени, выявляют направление развития, измеряют интенсивность развития. Рассчитывается относительная величина динамики как отношение уровня признака в определенный период или момент времени к уровню того же признака в предшествующий период или момент времени, т. е. характеризует изменение уровня определенного явления во времени.
4. Относительные величины сравненияхарактеризуют количественное соотношение одноименных показателей, относящихся к различным объектам статистического наблюдения. Для сопоставления уровня цен на один и тот же товар, реализуемый через государственные магазины и на рынке, используются относительные величины сравнения. За базу сравнения принимается государственная цена.
5. Относительные величины координации– это разновидность показателей сравнения. Они применяются для характеристики соотношения между отдельными частями статистической совокупности. Относительные величины координации характеризуют структуру изучаемой совокупности.
6. Относительные величины интенсивностидемонстрируют, насколько широко распространено исследуемое явление в определенной среде, характеризуются соотношением разноименных и взаимосвязанных между собой абсолютных величин.
Относительная величина демонстрирует, сколько единиц одной статистической совокупности приходится на единицу другой статистической совокупности.
Комплексное использование абсолютных и относительных величин дает всестороннюю характеристику изучаемого явления.
32. Что представляют собой статистические ряды распределения и по каким признакам они могут быть образованны?
Статистические ряды распределенияпредставляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку. Они характеризуют состав (структуру) изучаемого явления, позволяют судить об однородности совокупности, границах ее изменения, закономерностях развития наблюдаемого объекта.
Ряды распределения, образованные по качественным признакам, называют атрибутивными. Например, распределение работников торговли по занимаемой должности, профессии, образованию; распределение товарооборота по формам торговли, товарным группам; распределение работников по возрасту, стажу работы, производительности труда, заработной плате и другим признакам. При группировке ряда по количественному признаку получаются вариационныеряды. При этом вариационные ряды по способу построения бывают дискретными (прерывными), основанными на прерывной вариации признака (например, число касс в магазине, комнат в квартире), и интервальными (непрерывными), базирующимися на непрерывно изменяющемся значении признака, имеющими любые (в том числе и дробные) количественные выражения (объем товарооборота, величина фонда оплаты труда, выработка продавца). В практике применяются также и интервальные ряды распределения. При их построении возникают вопросы о числе групп, величине интервала, его границе.
33. Как подразделяются вариационные ряды и на каких признаках они основаны?
При группировке ряда по количественному признаку получаются вариационныеряды. При этом вариационные ряды по способу построения бывают дискретными (прерывными), основанными на прерывной вариации признака (например, число касс в магазине, комнат в квартире), и интервальными (непрерывными), базирующимися на непрерывно изменяющемся значении признака, имеющими любые (в том числе и дробные) количественные выражения (объем товарооборота, величина фонда оплаты труда, выработка продавца).
34. Какова методика построения дискретных и интервальных рядов распределения? Приведите примеры.
Для построения дискретного ряда с небольшим числом вариантов выписываются все встречающиеся варианты значений признака, а затем подсчитывается частота повторения варианта. Ряд распределения принято оформлять в виде таблицы, состоящей их двух колонок (или строк), в одной из которых представлены варианты, в другой - частоты. Построение дискретного вариационного ряда не составляет труда.
Для построения ряда распределения непрерывно меняющихся признаков, либо дискретных рядов, представленных в виде интервалов ("от-до"), необходимо установить оптимальное число групп (интервалов), на которое следует разбить все единицы изучаемой совокупности. При группировке внутри однокачественной совокупности появляется возможность применения равных интервалов, число которых зависит от вариации признака в совокупности и от количества обследованных единиц.
Рассмотрим ряд распределения рабочих по стажу работы. При N=22, по формуле Стерджесса, число групп составит n=5. Зная число групп, определим интервал по формуле:
i = (xmax - xmin) / n = (11-2) / 5 = 1,8 ≈ 2
В результате получим следующий ряд распределения рабочих по стажу работы.
Таблица 7.1.1.
| Стаж работы (x) | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 |
| Число рабочих (f) |
35. Какова роль средних величин в регулировании действия случайных причин и определении среднего явления?
Средние величины позволяют сравнивать уровни одного и того же признака в различных совокупностях и находить причины этих расхождений.
В анализе изучаемых явлений роль средних величин огромна.
Средняя величина приобретает особую значимость в условиях рыночной экономики. Она помогает определить необходимое и общее, тенденцию закономерности экономического развития непосредственно через единичное и случайное.
36. Какие виды средних величин применяются в статистике?
Один из наиболее распространенных видов средней – средняя арифметическая,которая исчисляется тогда, когда объем ос–редняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.
Для вычисления средней арифметической величины сумму всех уровней признака делят на их число.
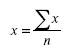
Средняя гармоническая.Для того чтобы определить среднюю арифметическую, необходимо иметь ряд вариантов и частот, т. е. значения х и f.