I Определение касательной и нормали к кривой

В курсе геометрии вы уже встречались с понятием касательной, а именно, касательная к окружности определялась как прямая, лежащая в одной плоскости с окружностью и имеющая с ней единственную общую точку. Однако такое определение неприменимо для случая произвольной кривой.

Так, например, оси и имеют по одной общей точке с параболой (рис. 4)

Рис. 4

 

Однако ось – касательная к параболе, а ось не является касательной к ней. Определим касательную к кривой точке в общем случае.

Пусть 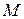– некоторая точка кривой , отличная от (рис 5).

Рис. 5

 

Прямая , проходящая через точки и 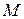, называется секущей кривой .

Если точку 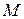перемещать по кривой , приближая к точке , то секущая будет поворачиваться вокруг точки , занимая соответственно положения , , и т.д.

Если секущая будет стремиться занять некоторое предельное положение при стремлении точки 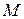вдоль кривой к точке , то прямая называется касательной к кривой .

Заметим, что не всякая кривая в любой точке имеет касательную. Простейшим примером такой кривой может служить график функции (рис. 6)

Рис. 6

Эта кривая в точке не имеет касательной.

 

Прямая, проходящая через точку , перпендикулярно касательной к кривой в точке , называется нормалью к кривой в точке .

Например, если прямая – касательная к кривой в точке , то прямая , , является нормалью к данной кривой (рис 7).

Рис. 7