Предел функции в точке
Обратимся к рисунку на экране.
Из рисунков видно, что при х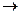 
3 функция (х – 3)2 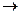0, т.е. бесконечно малая, значит функции вблизи т. aстановятся малыми по модулю.
Пример бесконечно малой функции
1)
| x | 3,1 | 3,01 | 3,001 | 2,9 | 2,99 | 2,999 | ||||||||||
| (x-3)2 | 0,01 | 0,0001 | 0,000001 | 0,01 | 0,0001 | 0,000001 | ||||||||||
| ||||||||||||||||
| x | 2,9 | 2,99 | 2,999 | 3,001 | 3,01 | 3,1 | 
| |||||||||
| 5,9 | 5,99 | 5,999 | 6,001 | 6,01 | 6,1 | 
| |||||||||
Определение.Число b называется пределом функции 
при 
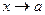, если для любого 
>0 вблизи точки a будет выполнятся неравенство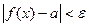 
(1) или: число b – есть предел при 
, если существует проколотаяокрестность точки a, в которой выполняется неравенство (1).
Аналогично, рассматривается вопрос о пределах односторонних (как при и 
), т.е. 
и 