Функциональное представление геометрических объектов. Понятие об R-функциях. Теоретико-множественные операции и биективные преобразования.

Неравенство (1) описывает подпространство в n-мерном эвклидовом пространстве. Равенство определяет сложную функцию n-1 переменной и описывает ориентированную поверхность размерности n-1. В трехмерном случае, объект, определенный неравенством обычно называется твердым телом (или объемом), а объект, определенный равенством называется сложной поверхностью. Функциональное представление объемов и поверхностей применяется для описания геометрии твердых тел, компьютерном дизайне, анимации, обработки рядов и объемной графики.

Определим геометрический концепт как тройка: (M, Ф, W), где M – набор геометрических объектов, Ф – набор геометрических операций и W – набор отношений между наборами объектов. С точки зрения математики такой набор есть алгебраическая система. Рассмотрим основные части этой тройки.

Два основных типа набора М – это простые геометрические объекты(примитивы) и комплексные геометрические объекты. Геометрический примитив описывается отдельно взятой функцией, выбранной из конечного набора возможных типов. Комплексный геометрический объект является результатом набора операций над примитивами. В системе моделирования, конечный набор примитивов может быть определен. Однако должна быть обеспечена возможность расширения этого набора в символьной манере.

Набор геометрических операцийФ включает такие операции, что 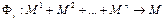, где n – число операндов в операции. Результатом операции является также объект из набора M, который обеспечивает замкнутость функционального представления. Пусть объект G₁ определен как 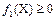. Для унарных операций объект говорят, что объект G₂ получен из объекта G₁ так, что G₂=Ф_i(G₁) и определен как 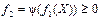, где непрерывная вещественная функция одной переменной. Примерами унарных операций может служить афинное преобразование, проекции, оффсетинг. Для бинарных операций говорят, что объект G₃ получен из G₁ и G₂ так, что G₃=Ф_i(G₁,G₂) и определен как , где непрерывная вещественная функция двух переменных. Примерами бинарных операций являются теоретико-множественные операции, блендинг. Теоретико-множественные операцииопределяются в аналитическом виде с помощью разработанной В.Л.Рвачевым теории R-функций. При этом результирующий объект включает граничные точки, что соответствует операциям трехзначной логики над предикатом принадлежности точки. Существует несколько систем R-функций, каждая из которых имеет свойство замкнутости. Наиболее часто используется следующая система:

для объединения , для пересечения . Здесь  =  (f₁,f₂) - произвольная непрерывная функция такая, что: -1 < (f1,f2)  1, (f1,f2) = (f2,f1) = (-f1,f2) = (f1,-f2); для вычитания . На практике используют два важных частных случая:=1; в этом случае , . Основное ограничение этих широкоизвестных минимаксных операций заключается в разрывности С¹ в точках, где f₁ = f₂, что может вызвать нежелаемые результаты при последующих операциях над объектом.=0; в этом случае , 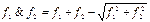. R-функции могут быть использованы для определения геометрических примитивов. Теоретико-множественные операции гладкого сопряжения(блендинг) генерируют сглаженные ребра конструктивных твердых тел с добавленным или удаленным материалом. Где R – соответствующая R-функция, d – функция смещения, принимающая максимальное значение d(0,0) и асимптотически стремится к нулю при увеличении значений ее аргументов. В частности, для d может быть предложено следующее выражение: 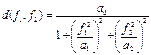, где a₀, a₁, a₂ – параметры, управляющие результирующей формой. Оффсетинг расширяет или сужает исходный объект. Виды: 1) Оффсетинг постоянного значения с F = f(X)+C, где отрицательная константа С характеризует отрицательный офсет, а положительная С – положительный офсет. 2) Оффсетинг вдоль нормали с F = f(X+DN) для положительного и F = f(X-DN) для отрицательного оффсетинга, где D – значение отклонения, а N – вектор градиента функции f в точке Х. 3) Оффсетинг постоянного радиуса с F = max(f(X’)) для положительного и F = max(f(X’)) для отрицательного оффсетинга, где Х’ – вектор координат точек, принадлежащих сфере данного радиуса D и с центром в точке X. Биективное отображениеслужит для определения деформаций исходных объектов. Пусть Ф_i определяется преобразованием координат: 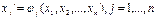, где - непрерывная вещественная функция. Предполагаем, что существует обратная функция . Получающийся в результате объект описывается как : . Примеры таких преобразований: изгиб, кручение, сжатие-расширение, а также отображение из цилиндрической в декартову систему координат. Афинные преобразования– важный частный случай биективного отображения. Пусть Ф_i – афинное отображение, определенное равенством X’=AX+C, где , , , и А={a_ij} – это матрица преобразования размерностью n*n и ненулевым определителем. Тогда 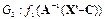. Это может быть движение вдоль прямой, вращение или масштабирование во времени. R-функции могут быть также использованы для приблизительного описания операции проекции из Eⁿ в E^n-1, не использующее обратное преобразование Ф^-1. Пусть будет определение функции для сечения. Тогда определение функции для проекции с может быть определено как f₂=f₁₁|f₁₂|…|f_1j|…|f_1N. Декартово произведение - это операция, увеличивающая размерность. , где 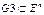и n=k+m. При помощи R-функций: . Метаморфозис- это бинарная операция над объектами, определенными в пространстве E^n-1. Результирующий объект определен в Eⁿ и описывается как взвешенная интерполяция между двумя определяющими функциями f₁ и f₂: , где g(x_n) - положительная непрерывная функция, g(x_n0) = 0, g(x_n1) = 1.

Преимущества функционального представления как основы для интерактивной системы моделирования:

1) Простота спецификации. Функциональное представление является замкнутым, единообразным, расширяемым.

2) Изображательность. F-rep рассматривается как используемый для обеспечения быстрой визуализации данных пользователя. Это достигается с помощью преобразования в полигональную сетку. Алгоритм полигонизации может быть разложен на отдельные составляющие для распараллеливания вычислений. Компактность F-rep позволяет запустить программы вывода изображений на машинах с не очень большим объемом распределенной памяти (как, например, транспьютеры).

3) Анализируемость. Для функционального представления достаточно просто применять геометрические запросы, как, например включение точки. Оно позволяет вычислять физические величины относительно формы (объемы, моменты инерции) при помощи известных алгоритмов.