Способы задания движения материальной точки скорость, ускорение
 Задать движение точки означает задать ее положение в каждый момент времени. Положение это должно определяться, как уже отмечалось, в какой-либо системе координат. Однако для этого не обязательно всегда задавать сами координаты; можно использовать величины, так или иначе с ними связанные. Ниже описаны три основных способа задания движения точки.
Задать движение точки означает задать ее положение в каждый момент времени. Положение это должно определяться, как уже отмечалось, в какой-либо системе координат. Однако для этого не обязательно всегда задавать сами координаты; можно использовать величины, так или иначе с ними связанные. Ниже описаны три основных способа задания движения точки.
Рис. 1
1. Естественный способ. Этим способом пользуются, если известна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве. При естественном способе необходимо задать (рис. 1):
а) траекторию движения (относительно какой-либо системы координат);
б) произвольную точку на ней нуль, от которого отсчитывают расстояние S до движущейся частицы вдоль траектории;
в) положительное направление отсчета S (при смещении точки М в противоположном направлении S отрицательно);
г) начало отсчета времени t;
д) функцию S(t), которая называется законом движения**) точки.
2. Координатный способ. Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание:
а) системы координат (не обязательно декартовой) q1, q2, q3;
б) начало отсчета времени t;
в) закона движения точки, т.е. функций q1(t), q2(t), q3(t).
Говоря о координатах точки, мы всегда будем иметь в виду (если не оговорено противное) ее декартовы координаты.
3. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку (рис. 2). В этом случае для описания движения необходимо задать:
а) начало отсчета радиус-вектора r;
б) начало отсчета времени t;
в) закон движения точки r(t).
Ускорение точки. , [м/сек2]. Проекции уск.-я: и т.д. Модуль уск.-я: , направляющ. косинусы: , и т.д.
При задании движения в полярных координатах: проекции ускорения на радиальное направление , поперечное направление , модуль ускорения . При естественным сп. задания движения полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения: . Модуль нормального ускорения: , r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории (^ к касательной) всегда к центру кривизны, т.е. в сторону вогнутости. Нормальное ускорение характеризует изменение скорости по направлению. Модуль касательного ускорения , направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движ-ии направление касат. уск. и скорости совпадают, при замедленном – противоположно. ^ , Þ . Вектор ускорения лежит в соприкасающейся плоскости Þ его проекция на бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в плоскости плоской кривой, бинормаль – ^ к главной нормали и касательной). Частные случаи движения точки:
1) Прямолинейное: радиус кривизны r= ¥ (бесконечно большой) Þ аn=0, a=at.
2) Равномерное криволинейное движ-ие: v=const Þ at=0, a=an. Уск. появляется только за счет изменения направления скорости. Закон движ-ия: s=s0+v×t, при s0=0 v=s/t.
3) Равномерное прямолинейное движ-ие: а=at=an=0. Единственное движ-ие, где а=0.
4) Равнопеременное криволинейное движ-ие: at=const, v=v0+at×t, . При равноуск. движении знаки у at и v одинаковы, при равнозамедленном – разные.
 13)Поступательным движением твердого тела называется такое его движение, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению во все время движения.
13)Поступательным движением твердого тела называется такое его движение, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению во все время движения.
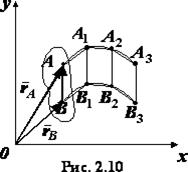
Теорема. При поступательном движении твердого тела все его точки движутся по одинаковым и параллельным траекториям и имеют в каждый данный момент времени равные по модулю и направлению скорости и ускорения.
Доказательство. Для доказательства теоремы рассмотрим движение отрезка прямой ,  проведенного в теле, совершающем поступательное движение (рис. 2.10). Из определения поступательного движения следует, что в каждый данный момент времени отрезок ,
проведенного в теле, совершающем поступательное движение (рис. 2.10). Из определения поступательного движения следует, что в каждый данный момент времени отрезок ,  занимающий последовательно положения
занимающий последовательно положения 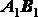 ,
,  ,
, 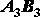 и т.д., остается параллельным своему первоначальному положению. Учитывая это и то что ,
и т.д., остается параллельным своему первоначальному положению. Учитывая это и то что , 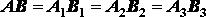 делаем вывод, что ломаные линии
делаем вывод, что ломаные линии 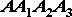 и
и 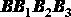 параллельны и при наложении совпадут всеми своими точками. При бесконечном уменьшении промежутков времени между рассматриваемыми положениями отрезка мы видим, что точка
параллельны и при наложении совпадут всеми своими точками. При бесконечном уменьшении промежутков времени между рассматриваемыми положениями отрезка мы видим, что точка 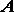 и точка
и точка 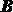 описывают одинаковые кривые, т. е. кривые, совпадающие при наложении.
описывают одинаковые кривые, т. е. кривые, совпадающие при наложении.
Для доказательства второй части теоремы заметим, что
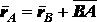
.(2.27)
Возьмем производные по времени от левой и правой частей
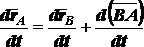
Так как , 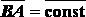 то .
то . 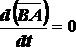
Тогда
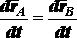

; (2.28)
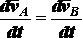

. (2.29)
Разобранная теорема позволяет сделать вывод, что поступательное движение твердого тела вполне определяется движением какой-либо одной его точки