курс магистратуры
Дополнения к моделям популяционной динамики экологических систем хищник-жертва
Выполнил: Файзуллин Р.Р.
курс магистратуры
Москва
2013 г.
Оглавление:
Введение 3
1 Классическая модель 3
2 Фенотипическая пластичность 4
3 Влияние эволюции 5
Заключение 7
Список литературы 7
Введение
В настоящее время задачи экологии имеют первостепенное значение. Важным этапом решения этих задач является разработка математических моделей экологических систем.
Одной из основных задач экологии па современном этапе является изучение структуры и функционирования природных систем, поиск общих закономерностей. Большое влияние на экологию оказала математика, способствующая становлению математической экологии, особенно такие её разделы, как теория дифференциальных уравнений, теория устойчивости и теория оптимального управления.
Одной из первых работ в области математической экологии была работа А.Д. Лотки (1880 - 1949), который первый описал взаимодействие различных популяций, связанных отношениями хищник - жертва. Большой вклад в исследование модели хищник -жертва внесли В. Вольтерра (1860 - 1940), В.А. Костицин (1883-1963) В настоящее время уравнения описывающие взаимодействие популяций, называются уравнениями Лотки — Вольтерра.
Уравнения Лотки - Вольтерра описывают динамику средних величин - численности популяции. В настоящее время на их основе построены более общие модели взаимодействия популяций, описываемые интегро-дифференциальными уравнениями, исследуются управляемые модели хищник - жертва.
Одной из важных проблем математической экологии является проблема устойчивости экосистем, управления этими системами. Управление может осуществляться с целью перевода системы из одного устойчивого состояния в другое, с целью её использования или восстановления.
1. Классическая модель
Попытки математического моделирования динамики как отдельных биологических популяций, так и сообществ, включающих взаимодействующие популяции различных видов, предпринимались давно. Одна из первых моделей роста изолированной популяции (2.1) была предложена еще в 1798 г. Томасом Мальтусом:
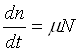, (1.1)
Данная модель задается следующими параметрами:
N — численность популяции;
— разность между коэффициентами рождаемости и смертности.
Наиболее серьезное исследование моделей биологических сообществ, включающих в себя несколько популяций различных видов, было проведено итальянским математиком Вито Вольтерра:
,
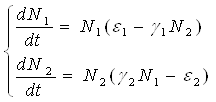где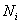 
— численность популяции;
— коэффициенты естественного прироста (или смертности) популяции;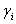 
— коэффициенты межвидового взаимодействия. В зависимости от выбора коэффициентов модель описывает либо борьбу видов за общий ресурс, либо взаимодействие типа хищник — жертва, когда один вид является пищей для другого.
2 Фенотипическая пластичность
Одними из явлений, обычно не включаемых в модель является влияние фенотипической пластичности видов и эволюция видов, входящих в систему. Фенотипическая пластичность это способность генома модифицировать фенотипическую экспрессию в ответ на условия окружающей среды: такие как температура, засуха, давление со стороны хищников и доступность ресурсов (Berg et al. 2010). Многие из функциональных черт, которые важны для конкуренции и соответствующего состава, сообществ являются высоко пластичными. Например, длина корней и демография корней сильно реагируют на количество питательных веществ, строение и количество листьев зависит от освещенности, механизмы защиты проявляются под давлением хищников. Уровень фенотипической пластичности черт может быть измерен нормой реакции, которая описывает изменение в значениях черт между экосистемами.
Рассматривая фенотипическую пластичность в функциональных чертах на уровне сообществ, можно сказать, что потребность в ресурсе и потребление ресурса являются пластичными чертами, которые могут изменить фундаментальную и экологические ниши вида в сообществе, если условия окружающей среды изменятся. Рассмотрим этот эффект на простом примере двух видов (Рис. 1). Фундаментальная ниша это уровни ресурсов А и В при котором виды могут выжить. Реализованные ниши уже фундаментальных вследствие перекрытия и конкуренции между видами. Под воздействием стресса оба вида показывают фенотипические различия в потреблении ресурса В. Однако виды различаются в пластичности, что отражается в скорости потребления ресурса В. Как результат, реализованные ниши изменяются под воздействием изменения факторов окружающей среды. Необходимо заметить, что фундаментальная ниша не изменяется. Этот пример без потери в общности можно обобщить на множественные факторы и большее количество видов.
Рис. 1, Роль фенотипической пластичности
3. Влияние эволюции
Одной из первых попыток объяснить регуляцию популяции через быстро изменяющийся генетический состав одной из популяций принадлежит Пиментелю(1961) и его математическому писанию «генетическому механизму обратной связи» в динамической системе растение-травоядное. Пиментель показал, что селекция, проводимая травоядным, может повлиять на генетический состав популяции растений, что в свою очередь влияет на плотности травоядных. Введение коэволюционной динамики – введение взаимных эволюционных изменений черт в двух взаимодействующих популяциях, является продолжением этих исследований.
Изменения экологических черт могут происходить с достаточной скоростью, чтобы влиять на взаимодействие видов. Возьмем для примера работу над насекомым-хозяином (зерновка четырёхпятнистая Callosobruchus maculatus) и паразитоидом (Heterospilus prosopidis) (Tuda 1998). В системе популяции составляющих видов осциллировали в течение 20 поколений и затем резко стабилизировались, причем плотность паразитоидов сократилась. Оказалось что, личинки насекомого выработали интерференционная конкуренцию (личинки убивали другие личинки населяющие тот же боб), тогда как в изначальной популяции присутствовала эксплуатационная конкуренция; атаки паразитоида не изменили свой характер. Также присутствовал компромисс между размером и выживаемостью и развитием личинок, подразумевая цену интерференционной конкуренции на развитие и выживаемости.
Похожий компромисс между усвояемостью и скоростью роста добычи есть в системе водоросли-коловратки (Fussmann et al. 2007). Несколько генотипов водорослей сосуществует и быстрая эволюция среди них в форме клонального отбора вызванного хищником имеет прямое влияние на динамику сообщества. Быстрая эволюция хищников происходила в системе водоросли-коловратки если выбирались клоны коловраток, которые репродуцировались асексуально над клонами, которые репродуцировались половым путем (Рис. 2). Модель не учитывающая в себя эволюцию коловраток не способна описать динамику системы.
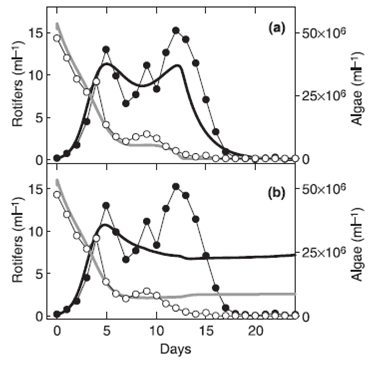
Рис. 2 Динамика в системе хищник-жертва. Черные и белые точки – численность коловраток и водорослей. Черная и серая линии модельное предсказание численности коловраток и водорослей.
Исследования показывают (Yoshida et al. 2007), что быстро эволюционирующие черты могут привести к динамике сообществ, которую нельзя наблюдать в устоявшихся сообществах.
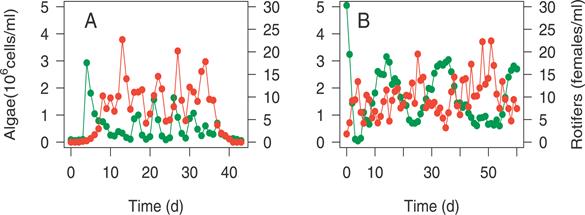
Рис. 3 Экспериментальные данные популяций водорослей(зеленый) и коловраток(красный) в Chemostat системе.
В случае А когда популяция водорослей произошла из одной клетки, а коловратки были введены достаточно быстро, чтобы благоприятные генотипы не могли возникнуть вследствие мутаций. В случае В популяция водорослей была получена из различных источников и генетически разнообразна. Когда генетическое разнообразие было исключено, в системе происходили классические циклы хищник-жертва, в которых за ростом численности жертв следует рост численности хищников с задержкой в четверть периода. Когда популяция жертв генетически гетерогенна и эволюционирует циклы дольше и практически не в фазе.
Заключение
В заключение была рассмотрена классическая модель хищник-жертва, а также дополнения к модели в виде фенотипической пластичности и эволюционной составляющей. Фенотипическая пластичность может объяснить многие явления в экологии сообществ, а в случаях, когда эволюция черт играет существенную роль в сообществах нельзя обойтись без включения ее роли в математические модели.
Список литературы:
1. А. Д. Базыкин, Математическая биофизика взаимодействующих популяций. / А. Д. Базыкин - М.: Наука, 1985. 181 с.
2. Berg, M.P, Trait plasticity in species interactions: a driving force
of community dynamics./ Berg, M.P. & Ellers, J. - Evol. Ecol.,2010, 24, 617–629.
3. Cortez M.H. Comparing the qualitatively different effects rapidly evolving
and rapidly induced defences have on predator–prey
interactions./ Cortez M.H. - Ecology Letters (2011) 14: 202–209
4. Fussmann, G.F. Eco-evolutionary dynamics of
communities and ecosystems./ Fussmann, G.F., Loreau, M. & Abrams, P.A. - Funct. Ecol., (2007), 21, 465–477.
5. Tuda, M. Evolutionary character changes and population responses in an
insect host-parasitoid experimental system./ Tuda, M. - Res. Popul. Ecol., (1998), 40, 293–299.
6. Yoshida, T. Cryptic population dynamics: rapid evolution masks trophic
interactions./ Yoshida, T., Ellner, S.P., Jones, L.E., Bohannan, B.J.M., Lenski, R.E. & Hairston,N.G. Jr. - PLoS Biology, (2007), 5, 1–12.