Аналитическое выравнивание ряда функцией параболы
Основная тенденция развития в рядах динамики со стабильными темпами прироста отображается функцией параболы второго порядка:
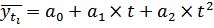 ,
,
где 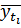 – средний уровень ряда;
– средний уровень ряда;
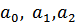 – параметры уравнения;
– параметры уравнения;
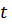 – обозначение времени.
– обозначение времени.
Показатели времени останутся такими же как в таблице 5.
Для вычисления параметров уравнения необходимо решить систему уравнений:
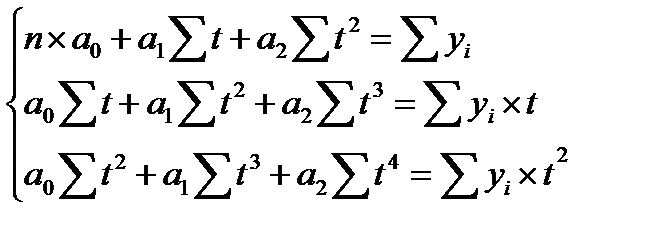
При условии, что 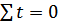 , система уравнений принимает вид:
, система уравнений принимает вид:
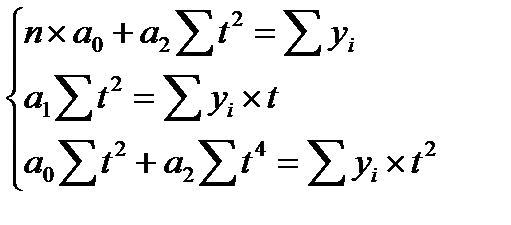
Необходимые величины расчитаны в таблице 7.
Таблица 7 – Расчётные данные для аналитического выравнивания по параболе второго порядка
| Месяц | Товарооборот фирмы, млн. руб.(  ) )
| 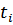
| 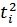
| 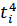
| 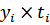
| 
| 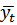
|
| Январь | -6 | -498 | 66,6 | ||||
| Февраль | -5 | -330 | 66,6 | ||||
| Март | -4 | -168 | 66,7 | ||||
| Апрель | -3 | -243 | 66,7 | ||||
| Май | -2 | -92 | 66,8 | ||||
| Июнь | -1 | -77 | 66,9 | ||||
| Июль | 67,0 | ||||||
| Август | 67,0 | ||||||
| Сентябрь | 67,1 | ||||||
| Октябрь | 67,2 | ||||||
| Продолжение таблицы 7 | |||||||
| Ноябрь | 67,2 | ||||||
| Декабрь | 67,3 | ||||||
| Итого | 803,0 |
Используя полученные значения, рассчитаем величины параметров уравнения: Отсюда следует, что:

где 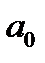 – параметр уравнения;
– параметр уравнения;
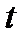 – обозначение времени;
– обозначение времени;
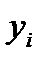 – уровень ряда;
– уровень ряда;
 – число уровней.
– число уровней.
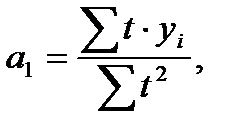
где 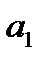 – параметр уравнения;
– параметр уравнения;
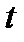 – обозначение времени;
– обозначение времени;
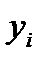 – уровень ряда.
– уровень ряда.
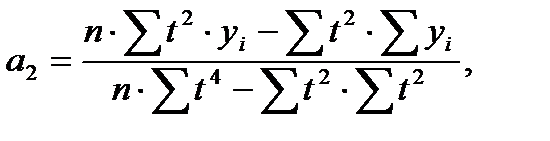
где  – параметр уравнения;
– параметр уравнения;
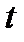 – обозначение времени;
– обозначение времени;
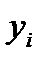 – уровень ряда;
– уровень ряда;
 – число уровней.
– число уровней.
Значения параметров:
 тыс. руб.,
тыс. руб.,
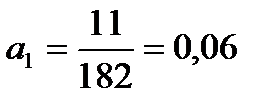 тыс. руб.,
тыс. руб.,
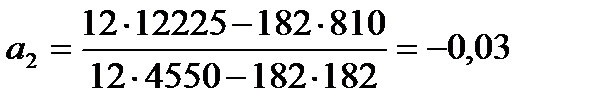 тыс. руб.,
тыс. руб.,
Значение параметров подставляем в исходное уравнение:
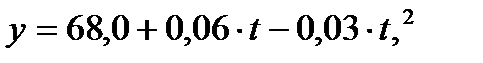
Отобразим графически эмпирические и теоретические уровни ряда.
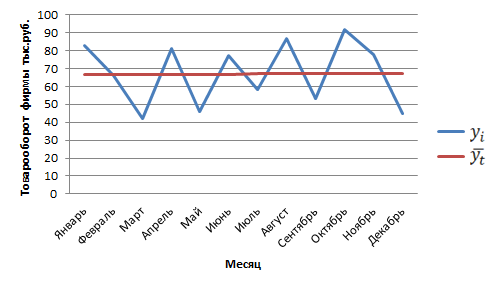
Рисунок 6 – Аналитическое выравнивание ряда функцией параболы
Рассчитаем стандартизированную ошибку аппроксимации:

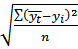 =
=  =
= 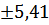
Таблица 8 – Расчетная таблица для определения стандартизированной ошибки аппроксимации
| Месяц | Товарооборот фирмы, тыс. руб. |
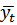
|
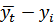
|
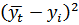
|
| Январь | 66,6 | -16,4 | 269,0 | |
| Продолжение таблицы 8 | ||||
| Февраль | 66,6 | 0,6 | 0,4 | |
| Март | 66,7 | 24,7 | 610,1 | |
| Апрель | 66,7 | -14,3 | 204,5 | |
| Май | 66,8 | 20,8 | 432,6 | |
| Июнь | 66,9 | -10,1 | 102,0 | |
| Июль | 67,0 | 9,0 | 81,0 | |
| Август | 67,0 | -20,0 | 400,0 | |
| Сентябрь | 67,1 | 14,1 | 198,8 | |
| Октябрь | 67,2 | -24,8 | 615,0 | |
| Ноябрь | 67,2 | -10,8 | 116,6 | |
| Декабрь | 67,3 | 22,3 | 497,3 | |
| Итого | 803,0 | -4,9 | 3527,3 |